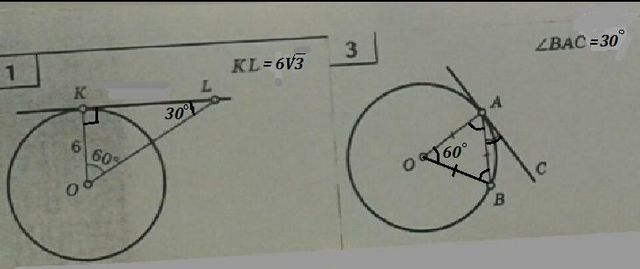
Объяснение:
1) ОК⊥KL ⇒ ∠OLK=90°-60°=30°
Катет, лежащий против угла в 30° , равен половине гипотенузы ⇒
OL=2*KO=2*6=12
По теореме Пифагора KL²=OL²-KO²=144-36=108 , KL=√108=6√3
3) Если ОА=АВ, причём ОА - радиус, то и другой радиус ОВ=ОА=АВ ⇒ ΔАОВ - равносторонний, все его углы равны 60° ⇒ ∠АОВ=60° .
∠АОВ - центральный, опирается на дугу АВ, значит между касательной АС и хордой АВ угол ∠ВАС равен половине центрального угла АОВ ⇒ ∠ВАС=60°:2=30° .
Или: ∠ВАС=∠ОАС-∠ОАВ=90°-60°=30° .