Найдите площадь фигуры. (фото). На опечатку не обращайте внимание. (не совпадает с...

$y=1-|x-1|$ - "угол" , ветви вниз, вершина в точке (1,1). Можно уравнение этого "угла" расписать на два уравнения :

$x\geq 1\; \; \Rightarrow \; \; |x-1|=x-1\; \; \Rightarrow \; \; y=1-(x-1)=-x+2$ - это правая ветвь "угла" - прямая,угол наклона к оси ОХ тупой, пересечение с осью ОХ в точке (2,0).

$x<1\; \; \Rightarrow \; \; |x-1|=-(x-1)=-x+1\; \; \Rightarrow \; \; y=1-(-x+1)=x$ - это левая ветвь "угла" - прямая, биссектриса 1 и 3 координатных углов.

Аналогично, $y=-1+|x-1|=\left \{ {{-1+(-x+1)=-x\; ,\; esli\; x<1} \atop {-1+(x-1)=x-2\; ,\; esli\; x\geq 1}} \right.$

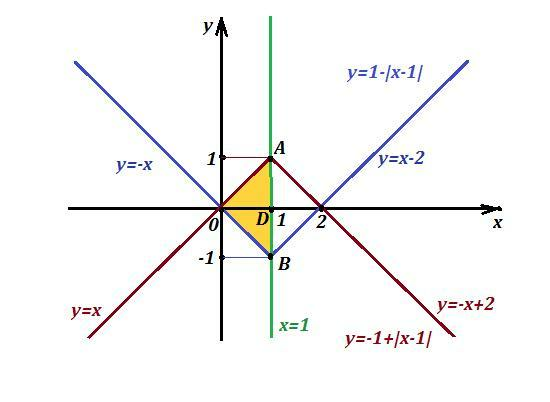
Проведём ещё прямую х=1, тогда получим треугольник, или слева от х=1, или справа от прямой х=1. Треугольники будут равными, поэтому выбираем любой для подсчёта площади. Я выбираю левый треугольник. Он ограничен прямыми у₁=х , у₂= -х , х=1 . Смотри рисунок.

Основание АВ у треугольника имеет длину 2, высота ОД =1 (видно из чертежа).

Площадь такого треугольника равна $S=\frac{1}{2}\cdot 2\cdot 1=1$ .

Через определённый интеграл площадь вычисляется так:

$S=\int\limits^a_b\, (y_1(x)-y_2(x))\, dx=\int\limits^1_0\, (x-(-x))\, dx=\int\limits^1_0\, 2x\, dx=\\\\=2\cdot \frac{x^2}{2}\, \Big |_0^1=1^2-0^2=1$

Найдите площадь фигуры. (фото). ** опечатку не обращайте внимание. (не совпадает с...