Ответ:
1,6B
Объяснение:
Для поля точечного заряда потенциал равен:
φ
То есть мы имеем функцию, обратно пропорциональную расстоянию до точечного заряда q.
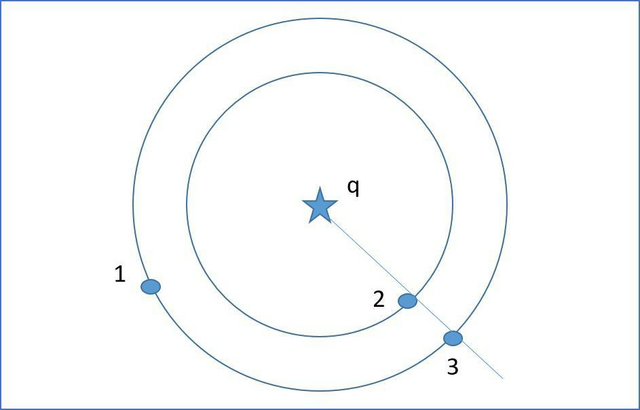
Есть такое понятие "эквипотенциальные линии", смотри картинку: потенциалы в точках 1 и 3 равны по 1В, а в точке 2 - 4В. И тут надо понимать, на мой взгляд, что условие задачи сформулировано некорректно. Ну посуди: вот середины отрезков 1 и 2, 1 и 3 явно имеют разный потенциал - они не лежат на одной эквипотенциальной окружности, хотя условию и набор 1,2, и набор 1,3 подходят. Так?
Вывод прост: в этой задаче можно рассматривать лишь случай в R1, то есть прямую. И заряд, и 2 точки лежат на одной прямой.
d_{1}/d_{2}=4, => \frac{d_{1} + d_{2}}{2}=\frac{5}{8}d_{1}" alt="1B=q/d_{1} , 4B=q/d_{2} , => d_{1}/d_{2}=4, => \frac{d_{1} + d_{2}}{2}=\frac{5}{8}d_{1}" align="absmiddle" class="latex-formula">
Тогда искомый потенциал:
φ
=1,6B
