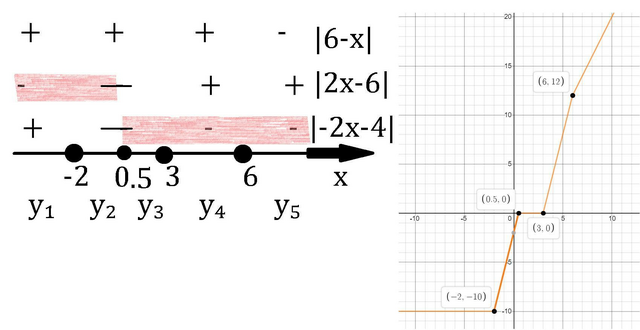
Это функция представляет из себя ломанную, нам надо найти нули этой функции. На числовой прямой отметим точки в которых аргументы модулей равны нулю. Таким образом мы сможем узнать как на промежутках раскрываются модули и выглядит функция, сверху напишу модули, чтобы было понятно, хотя можно сразу писать конечную функцию для промежутка. см. вниз.
Да и ||2x-1|-5| я представил как |2x-6| и |-2x-4|, при этом первый существует когда x>0.5, а другой когда x<0.5 т.к. 2x-1=0 =>x=0.5
Ординаты точек в которых происходит смена знака у модуля.
Можно построить график ломанной, а можно сразу по условию определить где функция будет равна 0.
Главное помнить, что функция 
существует на каком-то промежутку, а не при всех х.
Ответ: x∈[0.5;3].
