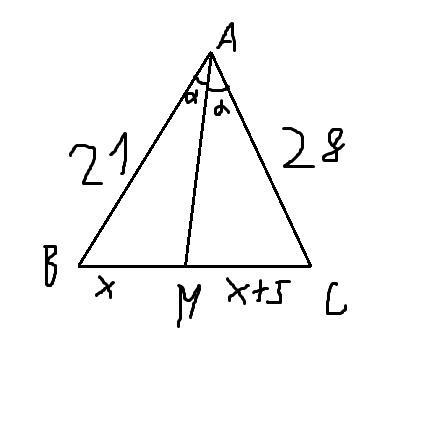Решить все 3 задачи(есть ещё 3 в предыдущем вопросе). Дам 60 баллов + лучший ответ за...

Ответ:

2.4) 1 2.5) 35 2.6) 64

Объяснение:

2.4)

$\frac{x}{x+2} + \frac{x+2}{x-2} = \frac{8}{x^2-4}\\\frac{x(x-2)}{(x+2)(x-2)} + \frac{(x+2)(x+2)}{(x+2)(x-2)} = \frac{8}{(x-2)(x+2)}\\x^2-2x+x^2 + 4x+4=8\\2x^2+2x-4=0\\x^2+x-2=0\\D = 1+2*4=9=3*3\\x_1=\frac{-1-3}{2}=-2\\x_1=\frac{-1+3}{2}=1$

x = -2 не подходит, при нем знаменатель обнуляется.

2.5)CM - BM = 5. Пусть BM = x, тогда CM = x + 5. Биссектриса делит угол A на два одинаковых угла a, высоты из вершины A, проведенные к BM, AM равны, так как BM и AM лежат на одной прямой, а значит

$S_{ABM} = \frac{1}{2} *AB*AM*sin\alpha \\S_{ACM} = \frac{1}{2} *AC*AM*sin\alpha \\\\S_{ABM} = \frac{1}{2}*BM*h\\S_{ACM} = \frac{1}{2}*CM*h\\$

Отсюда следует

$\frac{S_{ABM}}{S_{ACM}}=\frac{AB}{AC}= \frac{BM}{CM} \\\frac{21}{28}=\frac{x}{x+5}\\\frac{3}{4}=\frac{x}{x+5}\\ 3x+15=4x\\x=15\\x+5=20\\x+(x+5)=35$

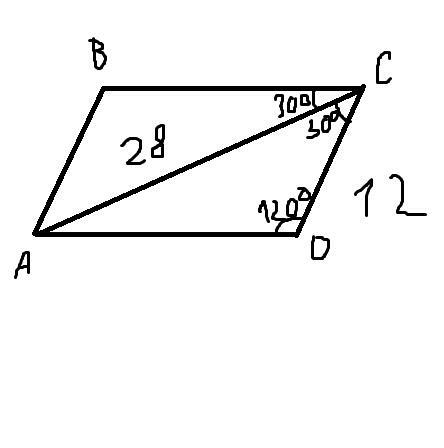
2.6) Воспользуемся теоремой косинусов для тр. ACD:

$AC^2=CD^2+AD^2-2*CD*AD*cos120\\28^2 = 12^2 + x^2 -2*12*x*(-0,5)\\x^2+12x-640=0\\D = 144+4*640=2704=52^2\\x_1=\frac{-12-52}{2} =-32 \\x_2=\frac{-12+52}{2} =20$

-32 < 0 - не подходит, так как длина может быть только > 0

Получается, что исходная сторона равна 20

P = 2(AD + CD) = 2(20 + 12)=64