Точка В лежит между точками А и С ** отрезках АВ и АС как ** диаметрах построенной...

Question

Точка В лежит между точками А и С на отрезках АВ и АС как на диаметрах построенной окружности. К отрезку АС в точке В проведен перпендикуляр до пересечения с большей окружностью в точке Д. Из точки С проведена касательная СК к меньшей окружности. Доказать , что СД = СК

Answer 1

Ответ:

Объяснение:

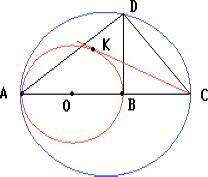
Пусть O — середина отрезка AB. В прямоугольном треугольнике ADC отрезок BD — высота, проведённая из вершины прямого угла. Поэтому DC2 = BC . AC. С другой стороны, по теореме о касательной и секущей CK2 = BC . AC. Следовательно, CD = CK.

---

Comments

Отметь как лучшее, если не сложно)