Сторона основания правильной треугольной призмы равна 24 см, боковое ребро равно 12 см....

Question

Сторона основания правильной треугольной призмы равна 24 см, боковое ребро равно 12 см. Найдите площадь сечения, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.

Answer 1

Ответ:

288 см²

Объяснение:

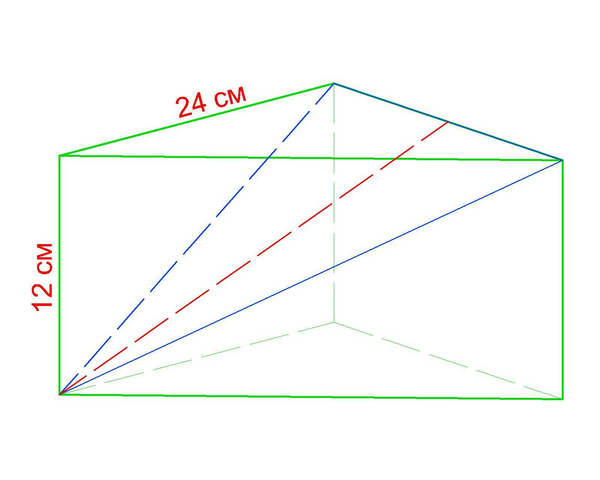
сечением здесь будет равнобедренный треугольник, с основанием, равным стороне основания призмы, и боковой стороной, которая является гипотенузой прямоугольного треугольника с катетами, равными высоте призмы и стороне ее основания.

Найдем боковую сторону сечения в=√(12²+24²)=√720 см.

Площадью треугольника сечения будет произведение его высоты на половину основания. Высота в свою очередь равна катету в прямоугольном  треугольнике с гипотенузой в и катетом 24/2=12 см.

Найдем высоту: н=√(720-12²)=24 см

тогда площадь сечения равна 24·12=288 см²

---

Comments

Или так: высота основания (высота правильного треугольника) h=(√3/2)*a = 12√3см. Высота сечения (гипотенуза треугольника с катетами - высотами основания и призмы) по Пифагору Н=√(12^2+12^2*3) = √(12^2(1+3))=12*2=24см. Sсеч= (1/2)*а*Н=(1/2)*24*24 = 288 см^2.

---

Тоже верно, но все же, если есть чертеж, я бы показал невидимые линии, где они уместны.)

---

Согласен.

---

Рисунок подправил. Уважаемый Юрий, считаю, что мой вариант на 1% более рационален, т.к. в нём не нужно выполнять дополнительных построений высоты равностороннего треугольника и высоты призмы в качестве катета. :))

---

И он бы был еще симпатичнее, если бы Вы не находили боковую сторону, а нашли бы квадрат этой стороны, ведь, сторона по сути, Вами не была использована для решения. А мне кажется, что имеет место быть любой способ. И у Юрия тоже своего рода, эксклюзив. Вот я бы никогда не додумался до него. Спасибо обоим.)