Пошаговое объяснение:
Дано: f(x) = (x² + 3*x + 1)².
Экстремум находится в корнях первой производной функции.
f'(x) = 2*(x²+3*x+1)*(x²+3*x+1)' = (4x+6)*(x²+3*x+1) = 0.
Находим корни производной.
4*х+6 = 0 и
х₁ = -6/4 = - 1.5 - корень
x² + 3*x + 1 = 0 - решаем квадратное уравнение.
D = 5.
x₂ = (-3 - √5)/2 (≈-2.618) x₃ = (-3 + √5)/2 (≈ - 0.382) - ещё два корня.
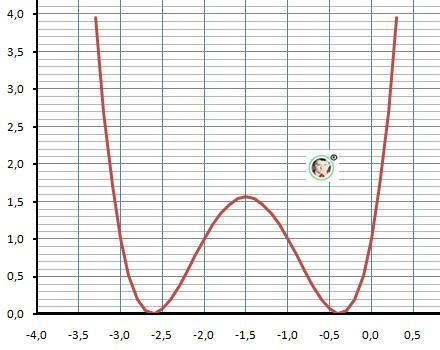
График функции на рисунке в приложении.
Экстремумы:
f(x₂) = f(x₃) = 0 - два минимума и
f(x₁) = f(1.5) = 1.5625 - максимум - ответ.