5) AM=CM, DM=BM, ∠AMD=∠CMB (вертикальные углы) =>
△AMD=△CMB (по двум сторонам и углу между ними)
∠DAM=∠BCM (соответствующие, то есть лежащие против равных сторон в равных треугольниках)
∠DAC и ∠BCA - внутренние накрест лежащие углы при пересечении прямых AD и BC секущей AC.
Если внутренние накрест лежащие углы равны, то прямые параллельны.
∠DAC=∠BCA => AD||BC (т.к. накрест лежащие углы равны)
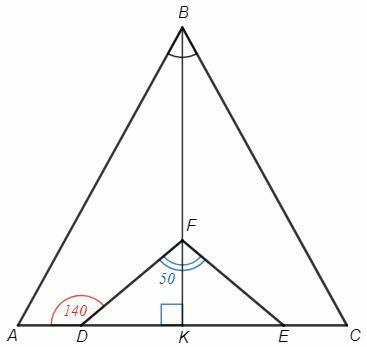
6) В равнобедренном треугольнике биссектриса, медиана и высота, проведенные к основанию, совпадают.
△ABC - равнобедренный, BK - биссектриса к основанию =>
BK - высота, ∠BKA=90
Если в треугольнике совпадают биссектриса и медиана, или биссектриса и высота, или медиана и высота, то треугольник равнобедренный.
В треугольнике DFE
∠FKD=90, FK - высота,
DK=EK, FK - медиана =>
△DFE - равнобедренный =>
FK - биссектриса, ∠DFK=∠DFE/2 =100/2 =50
Внешний угол треугольника равен сумме внутренних, не смежных с ним.
∠ADF=∠DFK+∠FKD =50+90 =140