Плоскости двух треугольников ABC и ABC1 образуют угол в 60°. Отрезок СС1,...

Question

Плоскости двух треугольников ABC и ABC1 образуют угол в 60°. Отрезок СС1, перпендикуля­рен плоскости треугольника ABC1, углы А и В которого равны соответственно 30º и 60°, а сторона AC1 равна 18 см. Вычислите площадь тре­угольника АВС.

Answer 1

Ответ: 108√3 см²

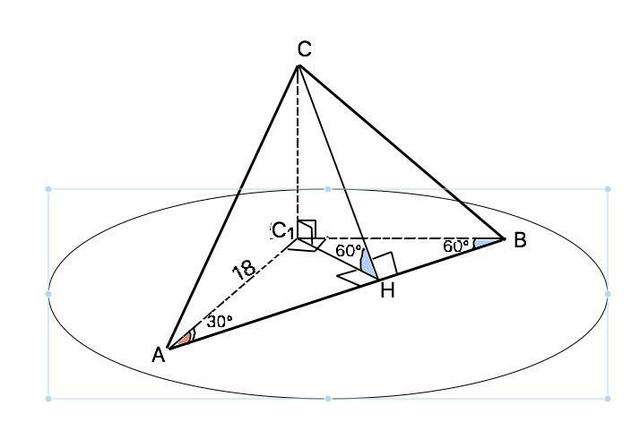
Объяснение: Угол между плоскостями данных треугольников –  двугранный. Его величина  определяется градусной мерой линейного угла, сторонами которого являются лучи, проведённые в его гранях перпендикулярно ребру с общим началом на нём. На приложенном рисунке СН - наклонная, С1Н - ее проекция, оба отрезка по т. о 3-х перпендикулярах перпендикулярны  АВ в одной точке и составляют между плоскостями треугольников ∠СНС1=60°.

Сумма двух углов ∆ АВС1 ∠А+∠В=30°+60°=90°. Из суммы углов треугольника третий ∠С1=180°-90°=90°. ⇒ ∆ АВС1 - прямоугольный. АВ=АС1:sin60°=18:(√3/2)=12√3 см

Из ∆ АНС1 отрезок С1Н=АС1•sin∠HAC1=18•1/2=9 см

Высота  СН ∆ АВС равна С1Н:cos∠CHC1=9:1/2=18 см

Ѕ(АВС)=СН•АВ:2=18•12√3:2=108√3 см²

                             

---