Ответ: 20√3 см².
Пошаговое объяснение:
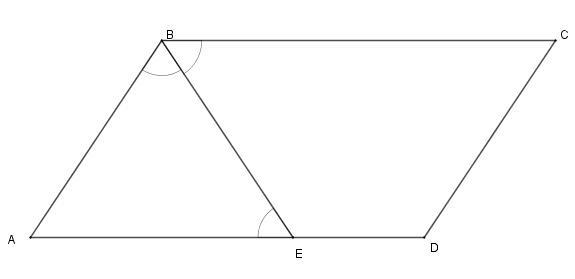
Бісектриса ВЕ ділить сторону AD на відрізки 5 см і 3 см, тобто
AE = 5 см і ED = 3 см. ∠ABE = EBC = 60° (оскільки ВЕ - бісектриса), тоді ∠CBE = ∠BEA як навхрест лежащі кути при AD || BC. Звідси ΔABE - рівнобедренний ⇒ AB = АE = 5 см.
AD = AE + ED = 5 + 3 = 8 см.
∠BAE = 180° - 60° - 60° = 60°
Площа паралелограма S = AD * AB * sin∠BAE = 8 * 5 * √3/2 = 20√3 см²