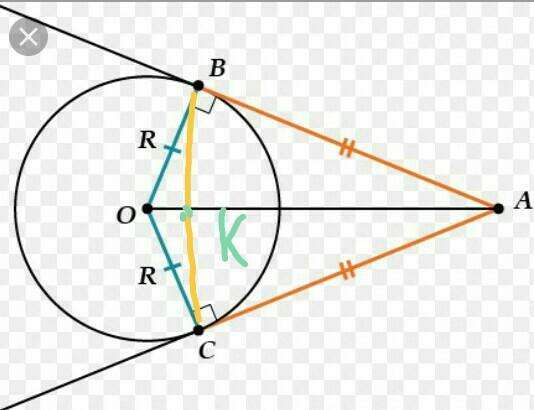
По свойствам касательных к окружности мы знаем, что АВ=ВС. Посмотрим на треуг. АВС: он равнобедренный и прямоугольный, значит АК - высота и бессиктриса => ∠ВАК=∠САК=45 градусов.
Рассмотрим треуг. АСО: угол С=90 градусов(т.к. радиус перпендикулярен касательной), угол СОА=180-90-45=45 градусов, значит, треугольник АСО - равнобедренный и АС=СО, а СО=ВО=R.
Рассмотрим четырехугольник АВОС: все стороны равны, ∠А=90 градусов, ∠В=90 градусов, ∠С=90 градусов, значит ∠О=90 градусов => АВОС-квадрат => АО=ВС=10 см.
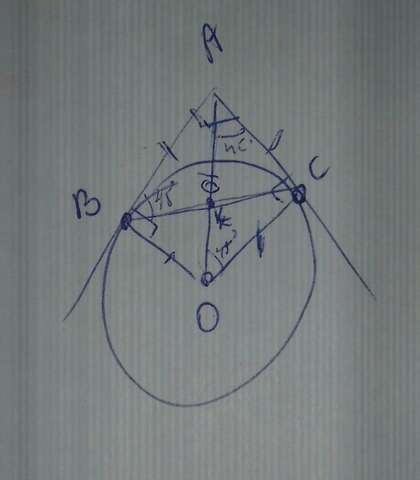
Вуаля;) Прикрепила картинку из интернета и нарисовала свою, чтобы понятнее было))) Удачи)
Ответ: 10 см.