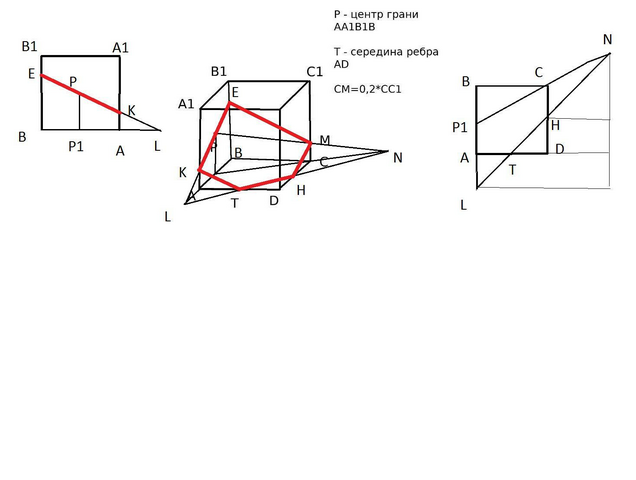
Пусть точка Р1 - это проекция точки Р на ребро АВ.
Основой построения является определение положения точки N, принадлежащей плоскости основания куба, как точки пересечения прямых РМ и Р1С.
Далее проводим прямую NT до пересечения с продолжением ребра АВ. Находим точку L, принадлежащую плоскости куба АВВ1А1.
Прямая NL пересекает ребро СД в точке Н.
Через точку Р проводим прямую LP, пересекающую рёбра АА1 и ВВ1 в точках К и Е.
Фигура сечения - пятиугольник ТКЕМН. Это ответ на 1 часть задания.
Для 2 части используются подобные треугольники.
Примем длину ребра куба, равную 10 (для кратности между 1/2 и 1/5).
Вначале находим отрезок EN: P1C = √(5² + 10²) = √125 = 5√5.
2/CN = 5/(5√5 + CN).
5CN =10√5 + 2 CN
CN = 10√5/3.
Далее раскладываем CN на 2 направления сторон основания с учётом соотношения 1/2 в подобном треугольнике Р1ВС
Получаем 10/3 и 20/3.
Следующим определяем длину отрезка AL тоже из подобия:
5/AL = (35/3)/(40/3). AL = 40/7. Отрезок DН = AL = 40/7.
Теперь переходим к плоскости АВВ1А1.
Аналогично определяем АК = 8/3 и ВЕ = 22/3.
Переходим к ответу на 2 часть задания.
Ребро ВВ1: (8/3)/(22/3) = 8/22 = 4/11.
Ребро АА1: (22/3)/(8/3) = 22/8 = 11/4.
Ребро СД: (30/7)/(40/7) = 30/40 = 3/4.
Остальные 2 ребра даны в задании.