Две прямые касаются окружности с центром О в точках А и В и пересекаются в точке Е....

Question

Две прямые касаются окружности с центром О в точках А и В и пересекаются в точке Е. Найдите угол между этими прямыми, если <ABO=50°.​

Answer 1

Ответ:100

Объяснение:

радиус проведёный в точку касания перпендикулярен касательной.

---

Comments

Не AOB, а ABO равен 50.

---

AEB=50*2=100

Answer 2

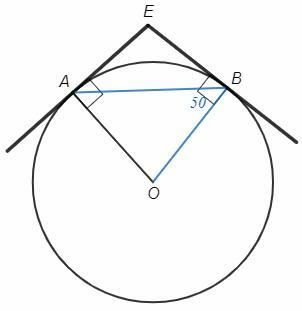
Радиус, поведенный в точку касания, перпендикулярен касательной. В четырехугольнике AEBO два противоположных угла 90, следовательно сумма двух других углов также 180.

AEB=180-AOB

Радиусы равны, треугольник AOB - равнобедренный, углы при основании равны.

2ABO=180-AOB

AEB=2ABO=50*2=100

---

Comments

да не заметил что там другой угол указан)