В трапеции ABCD с основаниями AD=12 и ВС=8, боковыми сторонами АВ=7 и CD=11 биссектрисы...

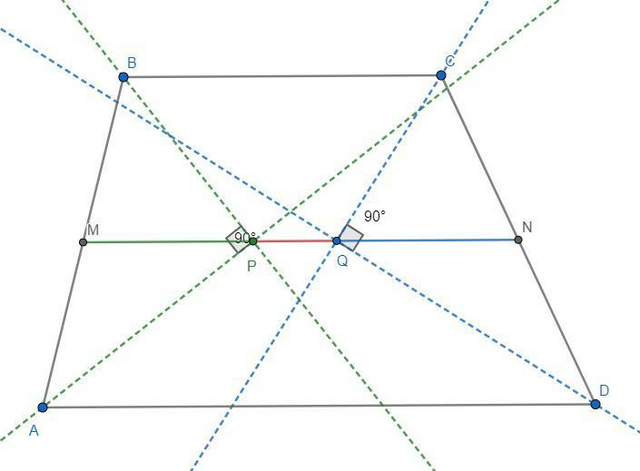
По свойству биссектрисы, она равноудалена от сторон которые её образуют.

Значит биссектриса из угла A равноудалена от сторон AD и AB, а биссектриса из угла B равноудалена от сторон AB и BC => точка пересечения биссектрис(P) равноудалена от сторон AB,AD и BC значит она лежит на средней линии трапеции (MN).

Аналогично точка Q лежит на средней линии трапеции.

-----------------

Рассмотрим треугольник ABP, как известно сумма односторонних углов трапеции=180°, значит сумма их половинок=90°.

Значит ∠APB=180-90=90°.

Аналогично ∠DQC=90°.

Отрезки PM и QN - это медианы опущенные из прямых углов, они равны половине гипотенузы.

---------------------

Искомый отрезок $PQ=|MN-PM-QN|=|\frac{AD+BC}{2}-\frac{AB}{2}-\frac{CD}{2}|=|10-9|=1$

----------------------

Ответ PQ=1