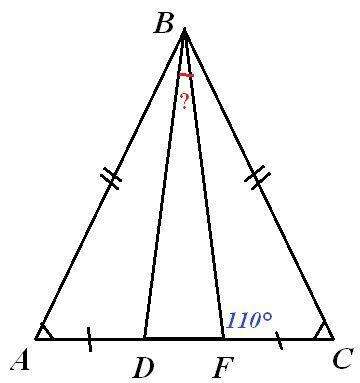
Ответ: 70°, 70°, 40°.
Пошаговое объяснение:
По свойству равнобедренного треугольника для ΔАВС с основанием АС ∠А=∠С. Тогда ΔABD=ΔCBF по двум сторонам и углу между ними (АВ=ВС, AD=СF, ∠А=∠С). Отсюда следует, что BD=BF. Тогда ΔDВА - равнобедренный с основанием DF. Поэтому в ΔDВF ∠D=∠F = 180°-110°=70° (т.к. ∠BFD + ∠BFC =180° как смежные). Наконец, по теореме о сумме углов треугольника в ΔDВF ∠D+∠F+∠B=180°, отсюда ∠B =180°-(70°+70°)=40°.
Итак, ∠BDF = ∠BFD = 70° , ∠DBF = 40°.