Ответ:
SH = a/(2Cosβ).
Объяснение:
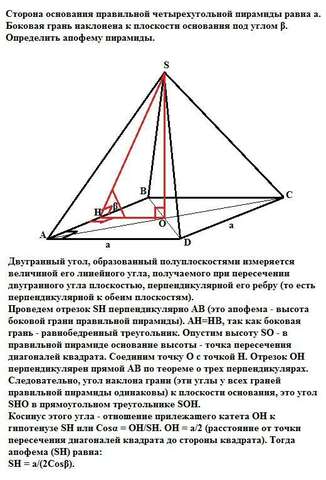
Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям).
Проведем отрезок SH перпендикулярно АВ (это апофема - высота боковой грани правильной пирамиды). АН=НВ, так как боковая грань - равнобедренный треугольник. Опустим высоту SO - в правильной пирамиде основание высоты - точка пересечения диагоналей квадрата. Соединим точку О с точкой Н. Отрезок ОН перпендикулярен прямой АВ по теореме о трех перпендикулярах.
Следовательно, угол наклона грани (эти углы у всех граней правильной пирамиды одинаковы) к плоскости основания, это угол SHO в прямоугольном треугольнике SOH.
Косинус этого угла - отношение прилежащего катета ОН к гипотенузе SH или Cosα = OH/SH. OH = a/2 (расстояние от точки пересечения диагоналей квадрата до стороны квадрата). Тогда апофема (SH) равна:
SH = a/(2Cosβ).