Ответ:
Объяснение:
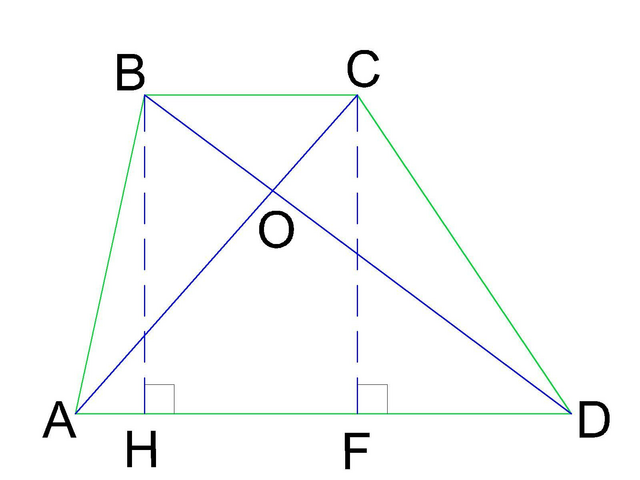
Побудуємо трапецію ABCD, та проведемо в ній діагоналі AС та BD, що перетинаються в точці О.
1) Проведемо в трикутниках ABD і ACD висоти BH і CF.
![\[{S_{\Delta ABD}} = \frac{1}{2}AD \cdot BK,\]](https://tex.z-dn.net/?f=%5C%5B%7BS_%7B%5CDelta%20ABD%7D%7D%20%3D%20%5Cfrac%7B1%7D%7B2%7DAD%20%5Ccdot%20BK%2C%5C%5D "\[{S_{\Delta ABD}} = \frac{1}{2}AD \cdot BK,\]")
![\[{S_{\Delta ACD}} = \frac{1}{2}AD \cdot CF.\]](https://tex.z-dn.net/?f=%5C%5B%7BS_%7B%5CDelta%20ACD%7D%7D%20%3D%20%5Cfrac%7B1%7D%7B2%7DAD%20%5Ccdot%20CF.%5C%5D "\[{S_{\Delta ACD}} = \frac{1}{2}AD \cdot CF.\]")
BK=CF (як висоти трапеції), відповідно,
![\[{S_{\Delta ABD}} = {S_{\Delta ACD}}\]](https://tex.z-dn.net/?f=%5C%5B%7BS_%7B%5CDelta%20ABD%7D%7D%20%3D%20%7BS_%7B%5CDelta%20ACD%7D%7D%5C%5D "\[{S_{\Delta ABD}} = {S_{\Delta ACD}}\]")
2) Аналогічно доводимо рівність площ ΔABC та ΔBCD:
![\[{S_{\Delta ABC}} = \frac{1}{2}BC \cdot BK,\]](https://tex.z-dn.net/?f=%5C%5B%7BS_%7B%5CDelta%20ABC%7D%7D%20%3D%20%5Cfrac%7B1%7D%7B2%7DBC%20%5Ccdot%20BK%2C%5C%5D "\[{S_{\Delta ABC}} = \frac{1}{2}BC \cdot BK,\]")
![\[{S_{\Delta BCD}} = \frac{1}{2}BC \cdot CF\]](https://tex.z-dn.net/?f=%5C%5B%7BS_%7B%5CDelta%20BCD%7D%7D%20%3D%20%5Cfrac%7B1%7D%7B2%7DBC%20%5Ccdot%20CF%5C%5D "\[{S_{\Delta BCD}} = \frac{1}{2}BC \cdot CF\]")
та
![\[{S_{\Delta ABC}} = {S_{\Delta BCD}}\]](https://tex.z-dn.net/?f=%5C%5B%7BS_%7B%5CDelta%20ABC%7D%7D%20%3D%20%7BS_%7B%5CDelta%20BCD%7D%7D%5C%5D "\[{S_{\Delta ABC}} = {S_{\Delta BCD}}\]")
![\[{S_{\Delta ABO}} = {S_{\Delta ABD}} - {S_{\Delta AOD}},\]](https://tex.z-dn.net/?f=%5C%5B%7BS_%7B%5CDelta%20ABO%7D%7D%20%3D%20%7BS_%7B%5CDelta%20ABD%7D%7D%20-%20%7BS_%7B%5CDelta%20AOD%7D%7D%2C%5C%5D "\[{S_{\Delta ABO}} = {S_{\Delta ABD}} - {S_{\Delta AOD}},\]")
![\[{S_{\Delta COD}} = {S_{\Delta ACD}} - {S_{\Delta AOD}}.\]](https://tex.z-dn.net/?f=%5C%5B%7BS_%7B%5CDelta%20COD%7D%7D%20%3D%20%7BS_%7B%5CDelta%20ACD%7D%7D%20-%20%7BS_%7B%5CDelta%20AOD%7D%7D.%5C%5D "\[{S_{\Delta COD}} = {S_{\Delta ACD}} - {S_{\Delta AOD}}.\]")
Так як площі трикутників ABD и ACD рівні (по вищедоведеному), то й
![\[{S_{\Delta ABO}} = {S_{\Delta COD}}\]](https://tex.z-dn.net/?f=%5C%5B%7BS_%7B%5CDelta%20ABO%7D%7D%20%3D%20%7BS_%7B%5CDelta%20COD%7D%7D%5C%5D "\[{S_{\Delta ABO}} = {S_{\Delta COD}}\]")
Таким чином, трикутники, утворені бічними сторонами та діагоналями трапеції, рівновеликі.
