Ответ:
Пошаговое объяснение:
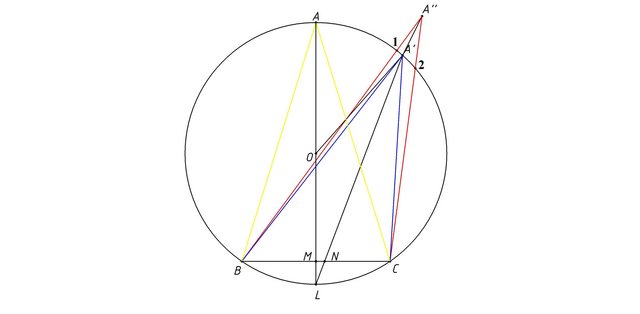
Пусть дан равнобедренный Δ ABC (AB=AC), опишем около него окружность, с центром в точке O, лежащей на его биссектрисе AM ,соответственно. Пусть биссектриса AM(она же высота ∠AMC=90°), пересекает дугу BC в точке L,деля ее на две равные дуги BL=LC.
Предположим, что существует точка A'' не лежащая на данной окружности,такая что ∠BA''C =∠BAC (рассматриваем пример когда точка вне круга)
Тогда ΔA''BC пересекает окружность в точках 1 и 2. Возьмем на дуге 12 Произвольную точку A' ,тогда у ΔA'BC ∠A'=∠A ,как углы вписанные в окружность и опирающиеся на одну дугу. ( точка A' лежит внутри ΔA''BC)
Очевидно что:
∠A'=360°-( 180°-(∠A'A''B+∠A'BA'') +180°-(∠A'A''C +∠A'CA'') )=
= (∠A'A''B+∠A'A''C) +∠A'BA'' +∠A'CA''=∠A'' +∠A'BA'' +∠A'CA''
Откуда: A=A'>A" ,то есть мы пришли к противоречию, не существует такой точки A". Аналогично доказывается невозможность того , что A'' находится внутри окружности, только в этом случае ,,опоясываем'' точку A'' треугольником A'BC ,то есть берем на стороне BC произвольную точку и проводим через эту точку и точку A" прямую,которая пересечет окружность в точке A',то есть эта прямая лежит внутри ΔA'BC, а на этой прямой точка A",то есть A" внутри ΔA'BC.
Таким образом геометрическое место точек A', таких что BA'=A это верхняя дуга BC.
P.S мы не рассматриваем точки что ниже стороны BC,тк для них можно провести симметричный относительно BC равнобедренный треугольник и провести те же рассуждения.
Докажем теперь, что для произвольной точки A' отличной от A (A' как доказано должно лежать на окружности)
биссектриса A'N
Заметим, что прямая A'N пересекает окружность в точке L,той же что и AM ,тк биссектриса любого угла делит дугу на которую он опирается пополам.
Рассмотрим ΔOA'L. OA'=OL=R -радиус окружности,откуда из неравенства треугольника:
OA'+OL>A'L OA'+OL=2R=AL
Вывод: AL>A'L
Так же очевидно ,что гипотенуза LN прямоугольного ΔLMN длиннее его катета LM:
LN>LM
AM=AL-LM
A'N=A'L-NL
AL-A'L>0
NL-LM>0
Cложим эти неравенства :
(AL-LM) -(A'L-NL)>0
AM-A'N>0
AM>A'N.
Таким образом из всех треугольников с данным основанием и данным углом при вершине наибольшую биссектрису угла при вершине имеет равнобедренный треугольник.
ЧТД.