Помогите решить задачу: В треугольника АВС прямая СD делит угол АВС в отношении 1:2....

Question

Помогите решить задачу: В треугольника АВС прямая СD делит угол АВС в отношении 1:2. Отрезки AD=DC=CB. Найдите углы треугольника.

Comments

Я решила её составив уравнение и получилось А=45, В=45, С=90

---

Но не уверена

---

Добрые люди помогите!

---

Еще раз проверьте условие, а потом просите помощи.

---

Вообще в треугольнике. Я ошиблась

---

Ищите и другую ошибку, нарисуйте чертеж, сами увидите, что она есть.

---

Ошибок быть не может. Потому что это олимпиадная задача

---

И чертеж у меня есть

---

CD делит угол если только ACB

---

Мне нужно хоть какое нибудь решение. Через 20 минут ВСЕ

Answer 1

Ответ:

30°, 60°, 90°

Пошаговое объяснение:

Если делит угол АСВ, то угол ADC = x; ∠DCB = 2x;

т.к. AD = DC, то ∠DAC = ∠DCA = x

тогда ∠ADC = 180° - x - x = 180° - 2x

∠CDB = 180° - (180° - 2x) = 2x

т.к. DC = CB, то ∠СDB = ∠CBD = 2x

треугольник DCB имеет три равных угла, значит, он равносторонний и все углы равны 60°

2х = 60°

х = 30°

∠А = 30°

∠В = 60°

∠С = 30° + 60° = 90°

Comments

Вы гений огромное спасибо

---

Вы спасли мне оценки

Answer 2

Ответ:

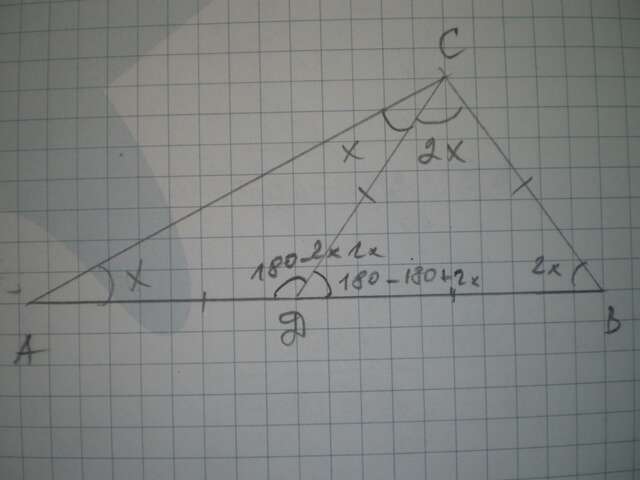
В треугольнике АВС прямая СD делит угол АСВ в отношении 1:2. Отрезки AD=DC=CB. Найдите углы треугольника .

Пошаговое объяснение:

Пусть ∠АСД=х°, тогда ∠СДВ=2х°.

ΔАСД - равнобедренный по условию, ∠А=∠АСД=х°.

Тогда ∠АДС=180-(х+х)=(180-2х)°

∠СДВ=180-(180-2х)=2х° по свойству смежных углов.

ΔСДВ - равнобедренный по условию, значит, ∠В=∠СДВ=2х°

Находим углы ΔАВС из уравнения

х+3х+2х=180

6х=180

х=30.

∠А=30°, ∠В=30*2=60°, ∠С=90°

---