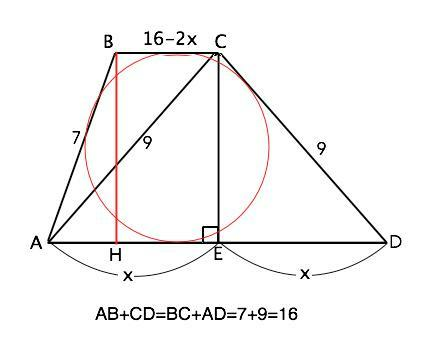
В трапеции ABCD боковые стороны равны 7 и 9, диагональ АС=9. Найти высоту СЕ, если АВ+СD=BC+AD
Ответ: 3√5 (ед. длины)
Объяснение:
ВС+АD=7+9=16 ∆ АСD равнобедренный, высота СЕ делит его на два равных треугольника.
Примем АЕ=ЕD=x . Тогда ВС=16-2х.
Из ∆ СЕD по т.Пифагора СЕ²=СD²-ED²=81-х²
Высота ВН=СЕ.⇒ ⎕НВСЕ - прямоугольник, НЕ=ВС=16-2х
АН=АЕ-ВС=х-(16-2х)=3х-16
Из ∆ АВН по т.Пифагора ВН²+АН²=АВ²
81-х²+(3х-16)²=49, откуда после некоторых преобразований и сокращения всех членов на 8 получим квадратное уравнение
х²-12х+36=0.
D=b2-4ac=-122-4·36=0.
Дискриминант равен нулю - уравнение имеет два одинаковых корня. х=-(-12):2=6
Вернемся к ∆ СЕD и по т.Пифагора найдём СЕ=√(81-36)=√45=3√5
* * *
Примечание:
Если суммы противоположных сторон четырехугольника равны, то в четырехугольник можно вписать окружность, при этом диаметр этой окружности равен высоте данной трапеции.