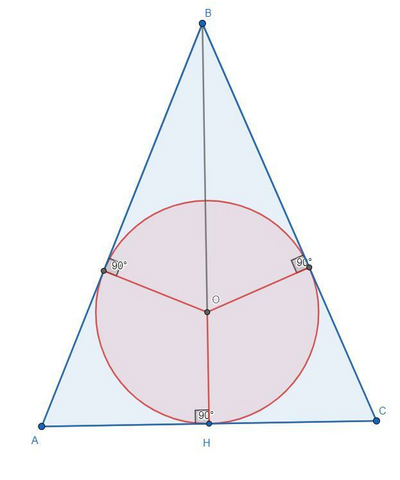
Дано:
ΔABC-равнобедренный;
основание AC=10;
высота BH=12;
---------------------
AB=BC по условию.
Опустим высоту BH, так-как треугольник равнобедренный, высота будет также являться медианой.
значит AH=HC=5.
из ΔABH найдем AB по теореме пифагора:

------------
найдем площадь треугольника ABC:

Также площадь можно высчитать как полупериметр умноженный на радиус вписанной окружности.

Найдем полупериметр:

Теперь найдем радиус:

Ответ: Радиус равен 10/3