Условие: медиана проведенная из вершины прямого угла треугольника равна половине...

Question

Условие: медиана проведенная из вершины прямого угла треугольника равна половине гипотенузе Дано:треугольник ABC, Угол B=90. BM медиана Доказать: BM=1/2 AC

Answer 1

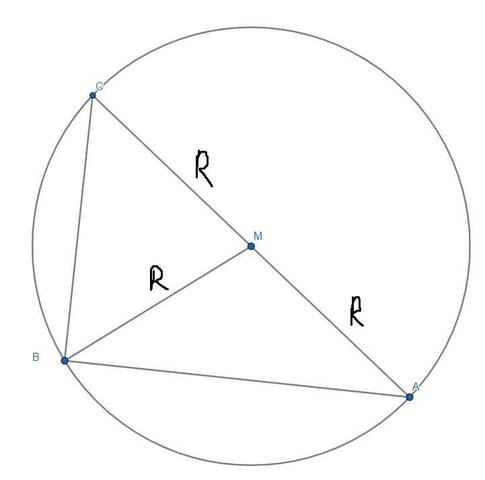
Опишем около треугольника окружность, так-как угол B прямой, он будет опираться на дугу 180°, значит он опирается на диаметр.

Центр окружности лежит на середине AC так-как туда падают серединные перпендикуляры треугольника.

значит:

AM=MC=BM как радиусы окружности.

отсюда:

---

Answer 2

Ответ:

ВМ =1/2АС

Объяснение:

Впишим прямоугольный треугольник в круг.

Так как медиана находиться на центре окружности(т. О) , то т. О делит медиану на 2 радиуса, то есть АО =ОС. ВМ- медиана, то есть тоже радиус, и значит О совпадает с М. ВМ=АО=СО, ВМ =1/2АС