По обратный теореме пифагора:

значит угол между сторонами AB и BC прямой.
-----------------
Если ∠ABC прямой ⇒ он опирается на дугу 180° ⇒ он опирается на диаметр ⇒ точка O середина гипотенузы и центр описанной окружности около треугольника ABC.
----------------
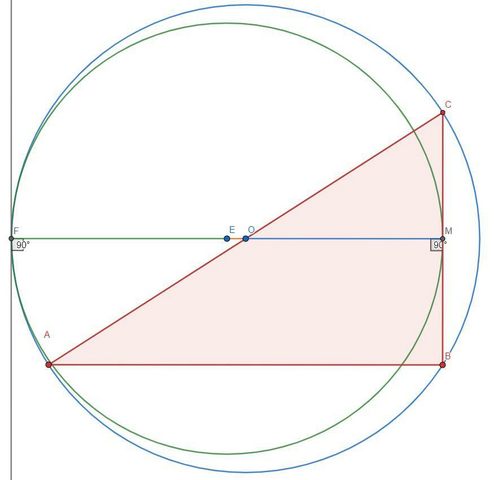
Проведем заданную окружность с центром в точке E (вообще существует 2 случая расположения этой окружности, но так-как от нас требуют найти максимальный радиус, другую окружность проводить не имеет смысла).
Пусть она касается катета BC в точке M и описанной окружности в точке F.
----------------
заметим что Отрезок OM образует прямой угол с катетом BC, так-как радиус опущенный на середину хорды всегда ей перпендикулярен.
Так-же EM⊥CB так-как, из условия, CB-касательная к окружности с центром в точке E.
Значит OM и EM параллельны или лежат на одной прямой, но они не могут быть параллельны так-как имеют общую точку M ⇒ точки M;O;E лежат на одной прямой.
Аналогично, OF и EF ⊥ общей касательной, значит они либо ║, либо лежат на одной прямой, но так-как они имеют общую точку F они не могут быть ║,значит они лежат на одной прямой.
Точки M;O;E;F лежат на одной прямой.
----------------------
Радиус окружности описанной около треугольника ABC равен половине гипотенузы AC=5.
Заметим что точка O и точка M являются серединами сторон AC и BC, значит отрезок OM- средняя линия треугольника и она равна половине AB=4.
------------------------
пусть радиус окружности которой нам надо найти=R, тогда:
R=OE+OM=OE+4
с другой стороны:
OF=OE+R=5 (так-как это радиус описанной окружности)
решим простую систему уравнений с 2м неизвестными:

Ответ 4,5