Ответ: 216 (ед. площади)
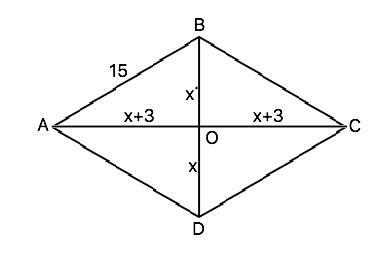
Объяснение: Ромб - параллелограмм, все стороны которого равны.
Диагонали ромба взаимно перпендикулярны и делят ромб на 4 равных прямоугольных треугольника, катеты которых равны половинам диагоналей.
Пусть в ромбе АВСD диагональ ВD=2х, АС=2х+6, тогда их половины ВО=х и АО=х+3. По т.Пифагора ВО²+АО²=АВ² х²+(х+3)²=225⇒
2х²+6х+9=225 ⇒ 2х²+6х -208=0 Сократив все члены уравнения на 2, получим приведённое квадратное уравнение х²+3х-208. Его корни можно найти через дискриминант, можно по т.Виета:
Сумма корней приведённого квадратного трехчлена равна его второму коэффициенту с противоположным знаком, а произведение - свободному члену ⇒
х1+х2=-3
х1•х2=-208 ⇒ корни равны 9 и -12 ( отрицательный корень не подходит)
х=9, 2х=18, 2х+6=24
Площадь ромба равна половине произведения его диагоналей.
Ѕ=18•24:2=216 (ед. площади)