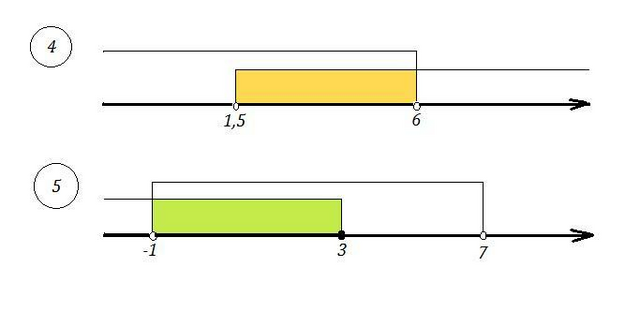
-2\; \; ,\; \; \; ODZ:\; 2x-3>0\; ,\; \; x>1,5\\\\log_{\frac{1}{3}}\, (2x-3)>log_{\frac{1}{3}}\; (\frac{1}{3})^{-2}\\\\0<\frac{1}{3}<1\; \; \Rightarrow \; \; \; 2x-3<9\; \; ,\; \; 2x<12\; ,\; x<6\\\\Otvet:\; \; x\in (1,5\; ;\; 6)\\\\\\5)\; \; log_5(x+1)\leq log_5(7-x)\; \; ,\; \; ODZ:\; \left \{ {{x+1>0} \atop {7-x>0}} \right. \; \to \; \; -11\; \; \Rightarrow \; \; \; x+1\leq 7-x\; \; ,\; \; 2x\leq 6\; \; ,\; \; x\leq 3\\\\Otvet:\; \; x\in (-1;3\, ]\; ." alt="4)\; \; log_{\frac{1}{3}}\, (2x-3)>-2\; \; ,\; \; \; ODZ:\; 2x-3>0\; ,\; \; x>1,5\\\\log_{\frac{1}{3}}\, (2x-3)>log_{\frac{1}{3}}\; (\frac{1}{3})^{-2}\\\\0<\frac{1}{3}<1\; \; \Rightarrow \; \; \; 2x-3<9\; \; ,\; \; 2x<12\; ,\; x<6\\\\Otvet:\; \; x\in (1,5\; ;\; 6)\\\\\\5)\; \; log_5(x+1)\leq log_5(7-x)\; \; ,\; \; ODZ:\; \left \{ {{x+1>0} \atop {7-x>0}} \right. \; \to \; \; -11\; \; \Rightarrow \; \; \; x+1\leq 7-x\; \; ,\; \; 2x\leq 6\; \; ,\; \; x\leq 3\\\\Otvet:\; \; x\in (-1;3\, ]\; ." align="absmiddle" class="latex-formula">
