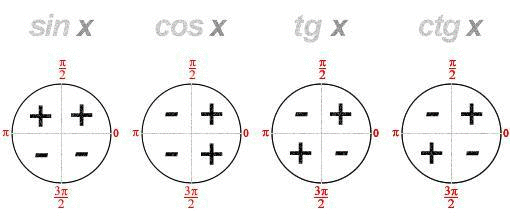
В первую очередь, определяем знаки функции:
0
По основным тригонометрическим тождествам, мы знаем, что:
tg(a)=\frac{1}{ctg(a)}=\frac{1}{\frac{1}{7}}=7 \\tg^2(a)+1=\frac{1}{cos^2(a)} => cos(a)=\sqrt{\frac{1}{tg^2(a)+1}}=\sqrt{\frac{1}{7^2+1}}=\sqrt{\frac{1}{50}}=\frac{\sqrt{2}}{10}=0,141\\sin^2(a)+cos^2(a)=1 => sin=\sqrt{1-cos^2(a)}=\sqrt{1-(\frac{\sqrt{2}}{10})^2}=\sqrt{1-\frac{1}{25}}=\sqrt{0,96}=0,9797" alt="ctg(a)*tg(a)=1 => tg(a)=\frac{1}{ctg(a)}=\frac{1}{\frac{1}{7}}=7 \\tg^2(a)+1=\frac{1}{cos^2(a)} => cos(a)=\sqrt{\frac{1}{tg^2(a)+1}}=\sqrt{\frac{1}{7^2+1}}=\sqrt{\frac{1}{50}}=\frac{\sqrt{2}}{10}=0,141\\sin^2(a)+cos^2(a)=1 => sin=\sqrt{1-cos^2(a)}=\sqrt{1-(\frac{\sqrt{2}}{10})^2}=\sqrt{1-\frac{1}{25}}=\sqrt{0,96}=0,9797" align="absmiddle" class="latex-formula">
