Ответ:
Объяснение:
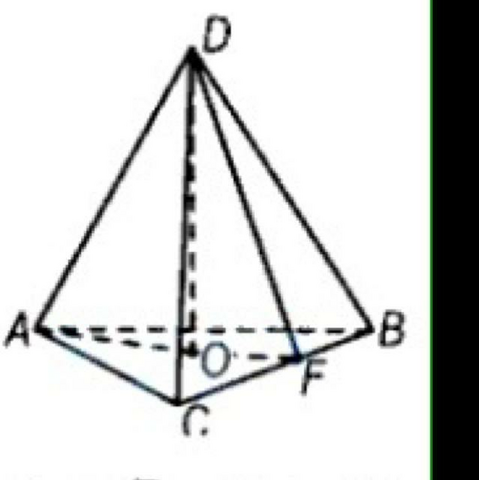
Так как боковые ребра пирамиды равны и углы между ними равны, то боковые грани тоже равны, значит ΔАВС правильный.
В прямоугольном тр-ке ВСД ДФ - высота и медиана, значит ВФ=СФ=ДФ.
ВС=СД√2=а√2 ⇒ ДФ=а√2/2.
Т.к. пирамида правильная, то высота, опущенная на основание, попадает в центр описанной и вписанной окружностей в самого основания.
ОФ=ВС√3/6=а√6/6.
В прямоугольном тр-ке ДОФ cosФ=ОФ/ДФ=(а/√6):(а/√2)=1/√3 - это ответ.