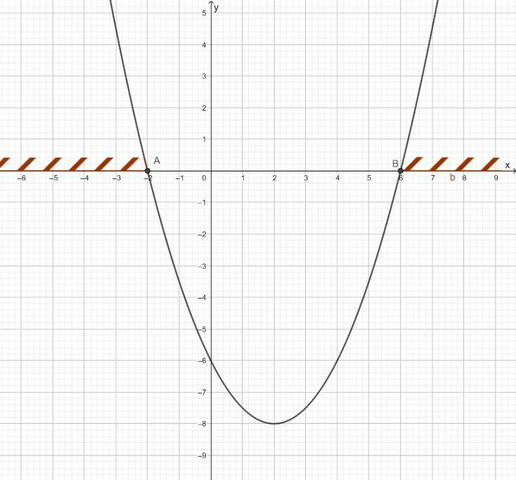
2) Функция y = 0,5x²-2x-6 квадратичная, график парабола, ветви вверх (коэффициент a = 0,5; a >0).
Вершина параболы x₀ = -b/2a = 2/1=2; y₀ = 0,5*4-4-6 = -8.
Пересечение оси y в точке x=0; y=-6.
Нули функции: y=0; 0,5x²-2x-6 = 0; D = b²-4ac = 4+12=16=4²;
x₁₂ = (-b±√D)/2a; x₁ = (2+4)/1=6; x₂ = (2-4)/1= -2.
График прилагается. y≥0 при x∈(-∞;-2]∪[6;∞)
Неравенство 0,5x²-2x-6≥0 выполняется при x∈(-∞;-2]∪[6;∞).
3) x²-x-6<0</p>
рассмотрим функцию f(x) = x²-x-6, квадратичная функция, график парабола, ветви вверх. Нули функции f(x) = 0; x²-x-6 = 0; D = b²-4ac =1+24 = 25 = 5²; x₁₂ = (-b±√D)/2a; x₁ = (1+5)/2=3; x₂ = (1-5)/2=-2.
f(x) = x²-x-6 = (x-3)(x+2)<0</p>
__+___(-2)___-___(3)___+___→x; f(x) = x²-x-6 < 0 при x∈(-2;3).
Целыми решениями неравенства x²-x-6<0 являются x = {-1; 0; 1; 2}</p>