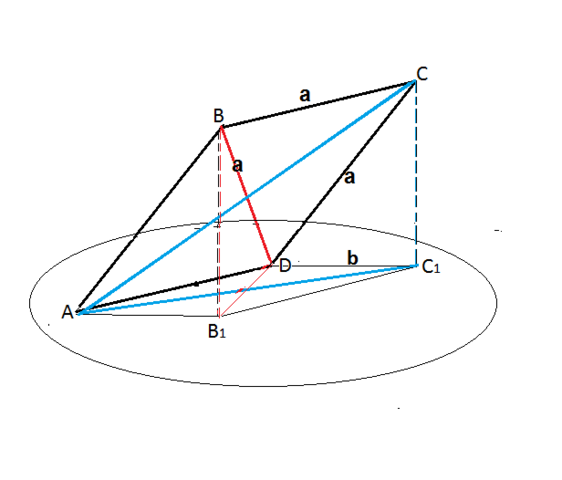
Так как в данном ромбе острый угол равен 60º, треугольник АВD - равнобедренный и равносторонний.
Диагональ ВD равна стороне ромба и равна а.
Диагональ АС равна двум высотам треугольника АВD.
АС=2*(а*sin 60º)=a√3
Проекцию АС₁ диагонали АС найдем из прямоугольного треугольника САС₁ по
т. Пифагора, где перпендикуляр СС1 - расстояние от С до плоскости.
СС₁=√(CD²-DC₁²)=√(а²-b²)
АС₁²=АС ²-СС₁²
АС₁²=(a√3)²-(а²-b²)=3а² - а²+b²= 2а²+b²
АС₁=√(2а²+b²)
Поскольку диагональ ВD равна стороне ромба, ее проекция ВВ₁ равна проекции стороны ромба и равна b.