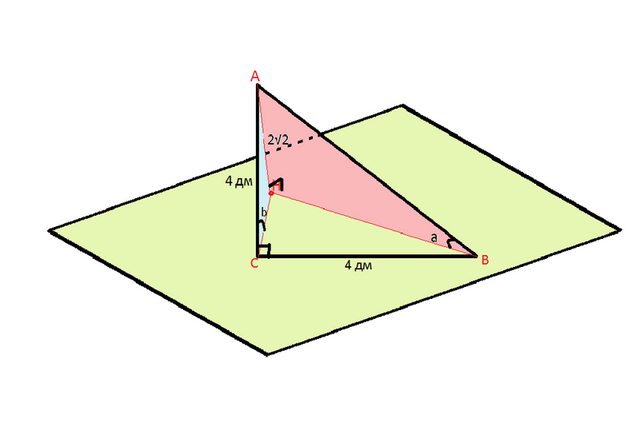
На рисунке плоскость α обозначена зеленым цветом.
Перпендикуляр к плоскости через точку А, пересекает плоскость в точке Н и равен 2√2.
1). Рассмотрим треугольник АСН, в нем:
АС=4 дм. - гипотенуза
АН= 2√2 дм - катет.
СН²=СА²-АН²=16-8=8
СН=2√2 дм
Надем тангенс угла АСН
tgЬ = АН/СН = 
угол b = 
2) Рассмотрим треугольник АВН, в нем:
АН= 2√2 дм
АВ = √(ВС²+АС²)=√32
ВН²=ВА²-АН²=32-8=24
ВН=√24=2√6
Надем тангенс угла АВН
tgа = АН/ВН =
угол а =