Пошаговое объяснение:
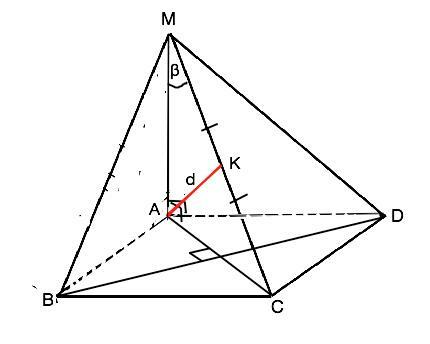
Сделаем рисунок согласно условию и обозначим пирамиду МАВСD. МА⊥АВСD
Из наклонных, проведенных из одной точки к плоскости больше та, у которой больше проекция. Поэтому наибольшее боковое ребро - ребро МС, проекцией которого является диагональ АС основания, => точка К - середина СМ, а отрезок АК=d
Формула объема пирамиды-
V=S•h/3, где Ѕ - площадь основания пирамиды, h - её высота.
Если одно из боковых рёбер пирамиды перпендикулярно основанию, то высотой пирамиды является это ребро. h=MA
Прямая, перпендикулярная плоскости, перпендикулярна любой прямой, лежащей в этой плоскости => МА⊥АС => угол АМС=β,
∆ АМС - прямоугольный, СК=МК, => АК - медиана и равна половине гипотенузы СМ (свойство медианы прямоугольного треугольника)
СМ=2АК=2d
Высота пирамиды MА=2d•cosβ
Диагонали квадрата равны и пересекаются под прямым углом. AC=BD=MC•sinβ=2d•sinβ
Площадь выпуклого четырехугольника равна половине произведения его диагоналей, умноженной на синус угла между ними.
S(ABCD)=AC•BD•sin90°:2=(2d•sinβ)²•1:2
S(ABCD)=4d²•sin²β:2=2d²•sin²β
V=2d²•sin²β•2d•cosβ/3=4d³•sin²β•cosβ/3