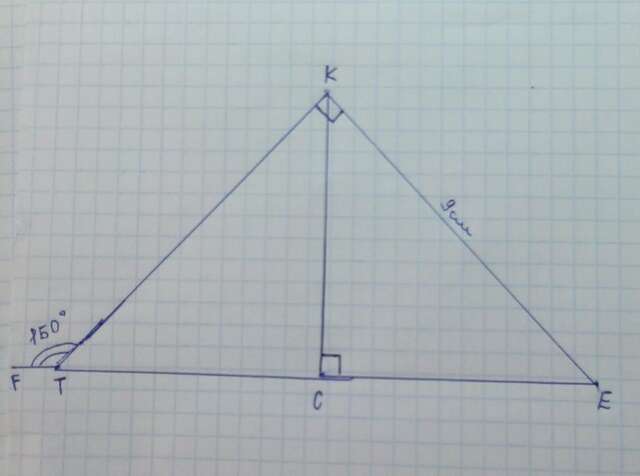
Дано:
△CKE - прямоугольный.
∠KTF = 150˚.
KE = 9 см вложение и
∠EKT = 90˚.
Найти:
∠C; CE.
Решение.
СУММА СМЕЖНЫХ УГЛОВ РАВНЯЕТСЯ 180°
∠KTF смежный с ∠KTC => ∠KTC = 180 - 150 = 30˚
∠C = 90˚, по рисунку.
СУММА УГЛОВ ТРЕУГОЛЬНИКА РАВНЯЕТСЯ 180°
=> ∠TKC = 180 - (90 + 30) = 60˚
Т.к. ∠EKT = 90˚ => ∠CKE = 90 - 60 = 30˚
ЕСЛИ ОСТРЫЙ УГОЛ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА РАВЕН 30°, ТО НАПРОТИВ ЛЕЖАЩИЙ КАТЕТ РАВЕН ПОЛОВИНЕ ГИПОТЕНУЗЫ.
=> CE = 9 : 2 = 4,5 см.
Ответ: 90°; 4,5 см.