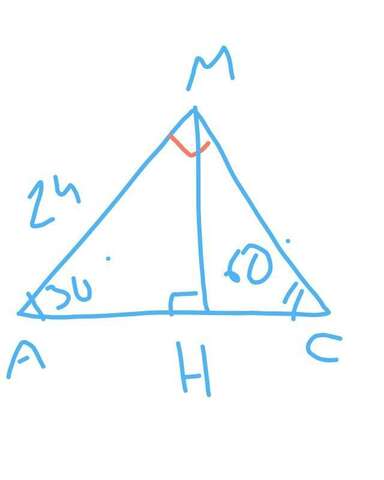
В равносторонем треугольнике медиана - это высота и биссектриса. Угол АМС равен 90°, а угол ВСА 60° (по свойству равностронего треугольника), тогда угол МАС = 90°-60° = 30°.
Проведём из точки М перпендикуляр к прямой АС. Это расстояние от точки М до стороны АС, его и будем искать.
Рассмотрим ∆АМН - прямоугольный. Против угла в 30 градусов лежит катет, равный половине гипотенузы. Поэтому, НМ = 24 см:2 = 12 см.
Ответ: угол МАС = 30°, расстояние от точки М до стороны АС = 12 см.