Область определения функции:






Применим свойство  и получаем следующее:
и получаем следующее:

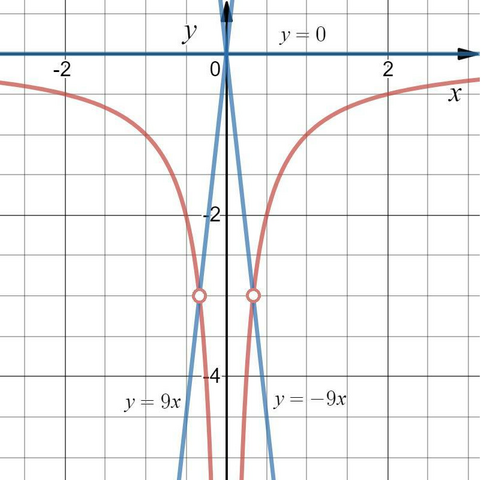
Следовательно, изобразим график функции  с учетом области определения (см. вложение).
с учетом области определения (см. вложение).
Прямая  — прямая пропорциональность — не будет иметь с графиком функции
— прямая пропорциональность — не будет иметь с графиком функции  ни одной общей точки (см. вложение), если:
ни одной общей точки (см. вложение), если:

Ответ: