4)
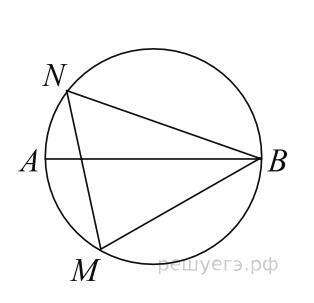
Угол NBA — вписанный, поэтому он равен половине дуги, на которую он опирается. Следовательно, дуга AN = 2∠NBA = 2*43 = 86. Диаметр AB делит окружность на две равные части, поэтому величина дуги ANB равна 180°. Откуда дуга NB = 180-86= 94. Угол NMB — вписанный, поэтому он равен половине дуги, на которую он опирается, то есть равен 94/2 =47.
5)
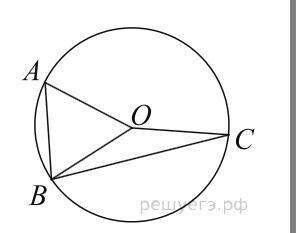
Проведём радиус OB. Рассмотрим треугольник AOB:
AO = OB, следовательно, углы ∠OAB = ∠ABO = 43 Рассмотрим треугольник BOC:
BO = OC, следовательно, ∠BCO = ∠OBC = ∠ABC − ∠ABO=75-43=32