В окружности с радиусом 8см проведена хорда длиной 8см. Чему равны длины стягиваемых ею...

Question

Дан 1 ответ

Хуqожнuк_zn · Answer 1 · 2020-06-05T19:38:52+0000

Ответ: Длина дуги AB равна 8π/3 см, длина дуги ACB равна 40π/3 см, площадь сегмента равна 16(2π/3 - √3) см².

Объяснение:

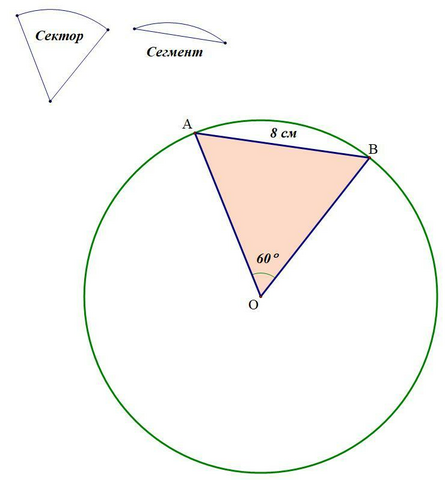
1. Проведём радиусы OA, OB. OA = OB = 8 см

2. AB = OA = OB ⇒ ΔABO -- равносторонний ⇒ ∠AOB = 60° (углы в р/ст треугольнике равны по 60°)

3. Градусная мера дуги AB = ∠AOB (центральный) = 60°

Градусная мера дуги AСB = 360° - 60° = 300°

4. Длина окружности вычисляется по формуле:

$l=2\pi R$

R -- радиус окружности

В нашем случае:

$l=2\pi \cdot OA=2\pi \cdot 8=16\pi\;cm$

5. Найдём, какую часть составляет дуга AB от всей окружности. Для этого надо найти отношение их градусных мер:

$\frac{\smile AB}{\smile ABA}= \frac{60^{\circ}}{360^{\circ}}=\frac{1}{6}$

Значит длина дуги AB в 6 раз меньше длины окружности, получаем:

$l_{\smile AB}=\frac{1}{6}\cdot l_{okp}=\frac{1}{6}\cdot 16\pi=\frac{8}{3}\pi\;cm$

6. Длину дуги ACB можно найти как 5/6 длины окружности или вычесть из длины окружности длину дуги AB:

$l_{\smile ACB}=l_{okp}-l_{\smile AB}=16\pi-\frac{8}{3}\pi=(\frac{48}{3}- \frac{8}{3})\pi=\frac{40}{3}\pi\;cm$

7. Чтобы найти площадь сектора, нужно найти SΔABO и площадь сектора. Площадь сектора находится следующим образом:

$S_{cekm}=\pi R^2\cdot \frac{n^{\circ}}{360^{\circ}}$

R -- радиус окружности, n -- угол сектора

$S_{cekm}=\pi \cdot OA^2\cdot \frac{\angle AOB}{360^{\circ}}=\pi \cdot 8^2\cdot \frac{60^{\circ}}{360^{\circ}}=\frac{8\cdot8}{6}\pi=\frac{32}{3}\pi\;cm^2$

Найдём площадь равностороннего треугольника ABO:

$S_{\Delta ABO}=\frac{a^2\sqrt{3}}{4} =\frac{OA^2\sqrt{3}}{4} =\frac{8^2\sqrt{3}}{4} =16\sqrt{3}\;cm^2$

8. Находим площадь сегмента как разность площадей сектора и треугольника:

$S_{c.}=S_{cekm}-S_{\Delta ABO}=\frac{32}{3}\pi-16\sqrt{3}=16(\frac{2}{3}\pi-\sqrt{3})\;cm^2$