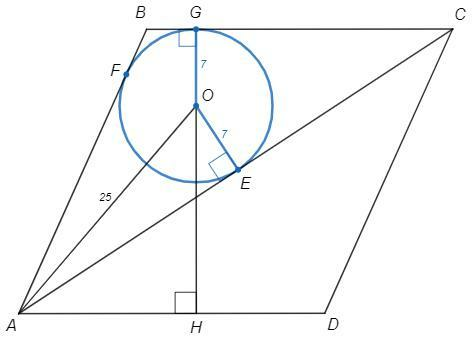
E, F, G - точки касания на сторонах AC, AB, BC
Отрезки касательных из одной точки равны.
AE=AF, BF=BG, CG=CE
p =AE+BG+CG =AE+BC (полупериметр)
Расстояние от точки до прямой измеряется длиной перпендикуляра.
Радиус в точку касания перпендикулярен касательной.
OE=OG =r =7
AE=√(AO^2 -OE^2) =24 (теорема Пифагора)
S(ABC) =pr =(24+BC)*7
Высота GH - расстояние между параллельными BC и AD - сумма расстояний от точки O до этих прямых.
GH =7+19 =26
S(ABCD) =BC*GH =BC*26
△ABC=△ABD (по трем сторонам) => S(ABC) =S(ABCD)/2
(24+BC)*7 = BC*26/2 => BC=28
S(ABCD) =28*26 =728