Объяснение:
а) 40°
б) 45°
в) 90°
Пошаговое объяснение:
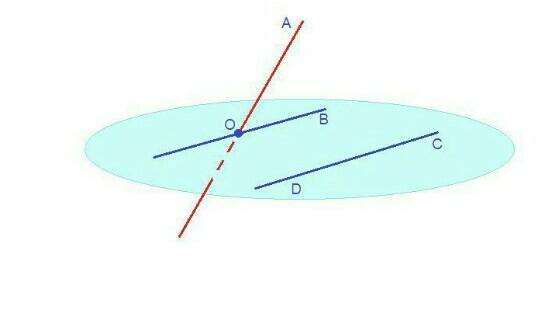
ОА и CD - скрещивающиеся,
ОВ ║ СD и ОВ пересекает ОА в точке О,
значит угол между прямыми ОА и ОВ и будет углом между скрещивающимися прямыми ОА и CD, т.е.
∠(ОА, ОВ) = ∠(ОА, CD)
Углом между пересекающимися прямыми считается угол, не превышающий 90°.
а) ∠АОВ = 40°, ⇒ ∠(ОА, CD) = 40°.
б) ∠АОВ = 135°, значит смежный с ним угол равен 180° - 135° = 45°, тогда ∠(ОА, CD) = 45°.
в) ∠АОВ = 90°, ⇒ ∠(ОА, CD) = 90°