Задачи по математике

Question

Дан 1 ответ

aliosha20_zn · Answer 1 · 2020-06-06T03:11:46+0000

Площадь фигуры ограниченной f(x) и g(x), которые пересекаются при x=а и x=b (a>b). При условии, что f(x)>g(x) на [b;a]. Вычисляется по формуле: $\int\limits^a_b {f(x)-g(x)} \, dx$

a)

f(x) = $\frac{1}{x^2}$ ; g(x)=0; a=-1; b=-3

S = $\int\limits^{-1}_{-3} {(\frac{1}{x^2} -0)} \, dx = \frac{-1}{x} \bigg| ^{-1}_{-3}=$ -1/(-1)-(-1/(-3)) = 1-(1/3) = 2/3

Ответ: 2/3 ед. кв.

б)

f(x)=x³+2; g(x)=0; a=2; b=0

S = $\int\limits^2_0 {(x^3+2-0)} \, dx =(\frac{x^4}{4} +2x)\bigg| ^{2}_{0} =$ (16/4)+4-(0/4+0)=8

Ответ: 8 ед. кв.

в)

f(x) = 2+x-x²; g(x) = x+2; a, b - ?

Решая уравнение 2+x-x²=x+2, получим, что x=0, то есть кривые касаются, они не ограничивают фигуру конечной площади. Они имеют только 1 общею точку. Площадь точки равна 0.

Ответ: 0.

г)

f(x) = 4x-x²; g(x)=0; a, b-?

4x-x²=0, x=0, x=4 т.к. дано, что x=5. Получаем a=5, b=4. f(x) = 4x-x² будет ниже g(x) при x∈[4;5]

S = $\int\limits^5_4 {(0-4x+x^2)} \, dx =(-2x^2+\frac{x^3}{3} )\bigg| ^{5}_{4} =$ (-2·25+125/3)-(-2·16+64/3) = 7/3

Ответ: 7/3 ед.кв.

д)

f(x) = 1-x; g(x)=3-2x-x²

1-x=3-2x-x²; x=1, x=-2. g(x) это парабола, ветви которой направлены вниз, и раз у кривых есть пересечение, то g(x) выше f(x) при x∈[-2;1]

S = $\int\limits^1_{-2} {(3-2x-x^2-1+x)} \, dx =\int\limits^1_{-2} {(2-x-x^2)} \, dx= \\(2x-\frac{x^2}{2} -\frac{x^3}{3} )\bigg| ^{1}_{-2} =$

= (2-1/2-1/3)-(-4-4/2+8/3) = 9/2

Ответ: 9/2 ед.кв.

е)

f(x) = x²-4x+6; g(x)=2; a, b - ?

x²-4x+6=2; x=2 - одно решение, откуда a=4; b=2. g(x) - касательная к f(x) поэтому f(x) выше g(x) при x∈[2;4]

S = $\int\limits^4_{2} {(x^2-4x+6-2)} \, dx =\int\limits^4_{2} {(x^2-4x+4)} \, dx= \\(\frac{x^3}{3} -2x^2+4x)\bigg| ^{4}_{2} =$

= (64/3-2·16+4·4)-(8/3-2·4+4·2) = 8/3

Ответ: 8/3 ед.кв.

є)

f(x)=x²; g(x)=1/x²; a,b - ?

x²=1/x²; x=±1. x>0 и x=2, поэтому a=2, b=1. При x>0 f(x) возрастает, g(x) убывает, поэтому f(x) выше g(x) при x∈[1;2]

S = $\int\limits^2_{1} {(x^2-\frac{1}{x^2} )} \, dx =(\frac{x^3}{3} +\frac{1}{x} )\bigg| ^{2}_{1} =$ (8/3+1/2)-(1/3+1) = 11/6

Ответ: 11/6 ед.кв.

ж) f(x)=1+0,5*cosx; g(x)=0; a=π/2; b=-π/2.

f(x) - чётная функция и g(x) тоже, поэтому S=2S'. b'=0

S' = $\int\limits^\frac{\pi}{2} _{0} {(1+0,\!5 \cos x-0)} \, dx =(x+0,\!5 \sin x)\bigg| ^{\frac{\pi}{2} }_{0} =$ π/2+0,5·1-0=0,5+π/2

S=2S'=1+π

Ответ: 1+π ед.кв.

з)

f(x)=sin2x; g(x)=x-π/2

sin2x=x-π/2; x=π/2 такой корень получается из нулей f(x) и g(x) больше пересечений не будет, это следует из |f(x)|≤1 и промежутков монотонности f(x) и g(x). a=π/2; b=0

f(x) выше g(x) при x∈[0;π/2], достаточно подставить любой x и убедиться в этом.

S = $\int\limits^\frac{\pi}{2} _{0} {(\sin 2x-x+\frac{\pi}{2} )} \, dx =(-0,\! 5\cos 2x-\frac{x^2}{2} +\frac{\pi}{2} x)\bigg| ^{\frac{\pi}{2} }_{0} =$ -0,5·(-1)-π²/8+π²/4-0 =0,5+π²/8

Ответ: π²/8 +0,5 ед. кв.

к)

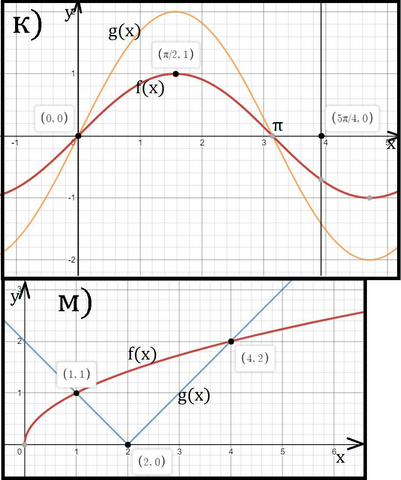
f(x)=sinx; g(x)=2sinx; a=5π/4; b=0

Построим f(x) и g(x) в одной координатной плоскости. g(x) это растянутое вдвое f(x) по оси ординат. Нули остались теми же. В итоге: f(x) ниже g(x) при x∈[0;π] и f(x) выше g(x) при x∈[π;5π/4]

S = $\int\limits^{\pi} _{0} {(2\sin x-\sin x)} \, dx +\int\limits^\frac{5\pi}{4} _{\pi} {(\sin x-2\sin x)} \, dx =\\ =\int\limits^{\pi} _{0} {(\sin x)} \, dx +\int\limits^\frac{5\pi}{4} _{\pi} {(-\sin x)} \, dx =(-\cos x)\bigg| ^{\pi}_{0} +(\cos x)\bigg| ^{\frac{5\pi}{4} }_{\pi} =$

= (1+1)+(-1/√2-(-1)) = 3-√2/2

Ответ: 3-(√2)/2 ед.кв.

м)

f(x)=√x; g(x)=|x-2|; a, b - ?

g(x) это ломанная с вершиной в точке (2;0).

√x = x-2; x=4

√x = -x+2; x=1

a=4; b=1. f(x) выше g(x). Интегрировать будет по частям, где g(x) возрастает, и где убывает.

S = $\int\limits^{2} _{1} {(\sqrt x+x-2)} \, dx +\int\limits^4_{2} {(\sqrt x-x+2)} \, dx =\\ =(\frac{2x^{3/2}}{3} +\frac{x^2}{2} -2x)\bigg| ^{2}_{1} +(\frac{2x^{3/2}}{3} -\frac{x^2}{2} +2x)\bigg| ^{4}_{2} =$

= (((4√2)/3+4/2-2·2)-(2/3+1/2-2))+((16/3-16/2+2·4)-((4√2)/3-4/2+2·2))) = 13/6

Ответ: 13/6 ед.кв.

л)

f(x)=cos2x; g(x)=0

cos2x=0; x=π/4+π/2·n, n∈Z.

По условию -π/4≤x≤π/4, поэтому a=π/4; b=-π/4

f(x) и g(x) это чётные функции, поэтому S=2·S'; b'=0

S' = $\int\limits^{\frac{\pi}{4} } _{0} {(\cos2x)} \, dx =(\frac{\sin2x}{2} )\bigg| ^{\frac{\pi}{4} }_{0} =$ sin(π/2)/2-0=0,5

S=2·0,5=1

Ответ: 1 ед. кв.