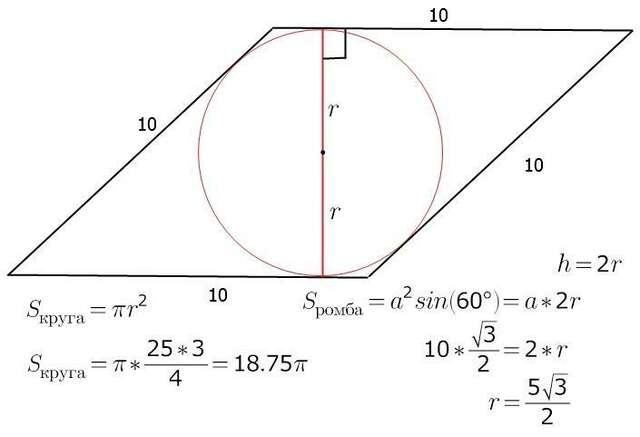
это радиус легко найти он равен высоте равен диаметр вписанного круга. Из точки пересечения диагоналей. диагонали делет на четыре равных прямоугольных треугольника раз один угол 60°то другой 120 ° диагонали ромба является биссектрисами его внутренных углов. Поэтому диагонали делят ромб на треугольники с углами 90° 60° 30° против угла в 30° лежит катет равным половине стороны ромба которая в этом треугольника является гипотенузой .
Поэтому катет равен 5 см . Высоту треугольника проведенную к стороне ромба ищем из треугольника с гипотенузы 5 см и противолежащим углом в 60°против гипотенузы лежит прямой угол равна 5 sin 60°
5× 3/2 площадь круга равна 25×3/4=75 п/4=18/75 /см/
По моему всё