Ответ: Всегда возможно, при любых чётных n.
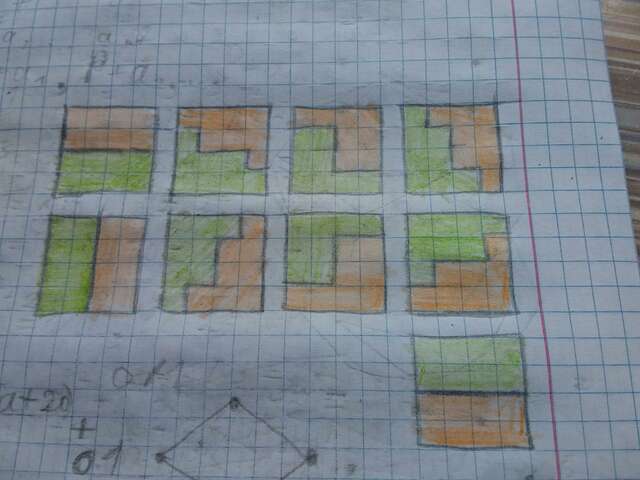
Решение: Найдём центр квадрата и поставим там точку. Проведём горизонтальный луч из него к левой стороне квадрата. Построим центральную симметрию этого луча относительно центра квадрата. Пусть "сверху" от прямой a красных и (n^2/2) - a зелёных клеток, тогда снизу будет a зелёных и (n^2/2) - a красных клеток. Немного переформулируем условие задачи: нужно вырезать такую фигуру из n^2/2 клеток (условие про равные фигуры будет соблюдаться), что разность количества красных и зелёных клеток в ней равна 0. Тогда во второй разность красных и зелёных клеток тоже равна 0, значит, количества зелёных клеток в них равны. Будем изменять тот луч, который мы проводили изначально, следующим образом: если в первых n/2 столбцах луч прямой, поднимем его на одну клетку в первом столбце, а если не прямой, поднимем его на одну клетку в месте спуска. Когда луч станет вертикальным, продолжим операции, мысленно повернув доску на 90 градусов. Каждый раз будем отражать этот луч центральной симметрией относительно центра квадрата (для n = 4 смотрите движения луча на картинке). После каждой операции будут получаться две равные фигуры. Заметим, что эта фигура получается из предыдущей добавлением одной клетки и убиранием другой. Значит, разность количества красных и зелёных клеток в фигуре либо изменяется на 2, либо не изменяется. Изначально разность чётная. После того, как мы закончили двигать луч, получилось, что исходные фигуры поменялись местами. Значит, разность количества красных и зелёных клеток поменяла знак (или не поменяла, если изначально была равна 0, но тогда задача уже решена). По дискретной непрерывности, найдётся операция, после которой разность была равна 0. Вот по ней и разрежем.