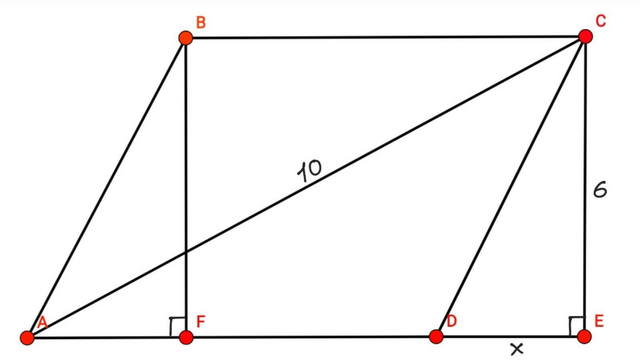
Дано: ABCD - ромб, АС= 10 см, BF - висота, BF⟂AD, BF= 6 см.
Знайти: S abcd
Розв'язання.
Продовжимо сторону ромба AD. Проведемо ще одну висоту з вершини С — висота СЕ⟂AD (див. рисунок)
СЕ=BF= 6 см.
У ΔACE (∠AEC=90°) за т.Піфагора:
АЕ²= АС²–СЕ²;
АЕ²= 10²–6²;
АЕ²= 100–36;
АЕ²= 64;
АЕ= 8 см (–8 не може бути)
У ромба всі сторони рівні. Тоді AD=DC.
Нехай DE= x см, тоді AD=DC= АЕ–DE= (8–x) см.
Тоді AD²=DC²= (8–x)² см.
У ΔDEC(∠DEC=90°) за т.Піфагора
DC²= DE²+CE²= x²+6²= x²+36.
Отримали рівняння:
(8–x)²= x²+36;
64–16x+x²= x²+36;
16x= 28;
x= 1,75
Отже, DE=1,75 см, тоді AD= 8–1,75= 6,25 см.
Площа ромба дорівнює добутку сторони на висоту.
S abcd = BF×AD= 6×6,25= 37,5 (см²)
Відповідь: 37,5 см².