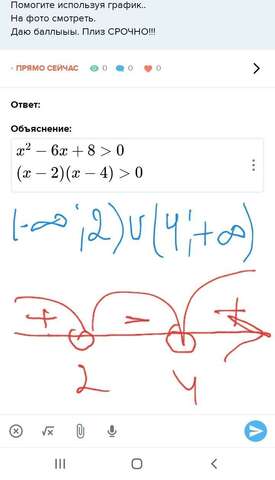
Объяснение:
х1 и х2 находим по теореме Виета
x1 = 2 \\ x2 = 4" alt="x1 \times x2 = 8 \\ x1 + x2 = 6 \\ = = > x1 = 2 \\ x2 = 4" align="absmiddle" class="latex-formula">
0 \\( x - 2)(x - 4) > 0 " alt=" 1){x}^{2} - 6x + 8 > 0 \\( x - 2)(x - 4) > 0 " align="absmiddle" class="latex-formula">
ответ(минус бесконечность;2)и (4;+бесконечность)
по теореме Виета находим корни
x1 = - 2 \\ x2 = - 4 \\ (x + 2)(x + 4) < 0" alt="x1 \times x2 = 8 \\ x1 + x2 = - 6 \\ = = > x1 = - 2 \\ x2 = - 4 \\ (x + 2)(x + 4) < 0" align="absmiddle" class="latex-formula">
ответ (-4;-2)
