Дана функция:

Найдём её производную:

Приравниваем производную к нулю:
![100 {x}^{99} - 500 {x}^{49} = 0 \\ {x}^{99} - 5 {x}^{49} = 0 \\ {x}^{49} ( {x}^{50} - 5) = 0 \\ x = 0 \\ {x}^{50} = 5 \\ x = 0 \\ x = ± \sqrt[50]{5} 100 {x}^{99} - 500 {x}^{49} = 0 \\ {x}^{99} - 5 {x}^{49} = 0 \\ {x}^{49} ( {x}^{50} - 5) = 0 \\ x = 0 \\ {x}^{50} = 5 \\ x = 0 \\ x = ± \sqrt[50]{5}](https://tex.z-dn.net/?f=100%20%7Bx%7D%5E%7B99%7D%20%20-%20500%20%7Bx%7D%5E%7B49%7D%20%20%3D%200%20%5C%5C%20%20%7Bx%7D%5E%7B99%7D%20%20-%205%20%7Bx%7D%5E%7B49%7D%20%20%3D%200%20%5C%5C%20%20%7Bx%7D%5E%7B49%7D%20%28%20%7Bx%7D%5E%7B50%7D%20%20-%205%29%20%3D%200%20%20%5C%5C%20x%20%3D%200%20%20%5C%5C%20%20%7Bx%7D%5E%7B50%7D%20%20%3D%205%20%5C%5C%20x%20%3D%200%20%5C%5C%20x%20%3D%20%C2%B1%20%5Csqrt%5B50%5D%7B5%7D%20)
Мы получили 3 точки возможного экстремума, причём
![- \sqrt[50]{5} < 0 < \sqrt[50]{5} - \sqrt[50]{5} < 0 < \sqrt[50]{5}](https://tex.z-dn.net/?f=%20-%20%20%5Csqrt%5B50%5D%7B5%7D%20%20%3C%200%20%3C%20%5Csqrt%5B50%5D%7B5%7D%20)
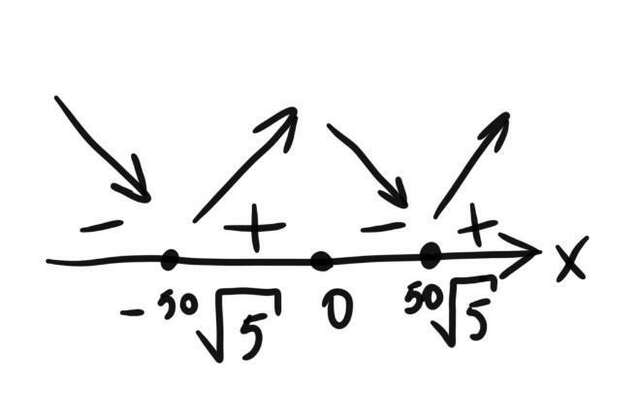
Разместим данные точки на координатной оси и найдём интервалы, где производная положительна/отрицательна что поможет нам найти где функция возрастает/убывает (рисунок приложен)
Исходя из рисунка получили 2 точки минимума:
![- \sqrt[50]{5} \: \: и \: \: \sqrt[50]{5} - \sqrt[50]{5} \: \: и \: \: \sqrt[50]{5}](https://tex.z-dn.net/?f=%20%20-%20%5Csqrt%5B50%5D%7B5%7D%20%20%5C%3A%20%5C%3A%20%20%D0%B8%20%5C%3A%20%20%5C%3A%20%20%5Csqrt%5B50%5D%7B5%7D%20)
Это и есть ответ.