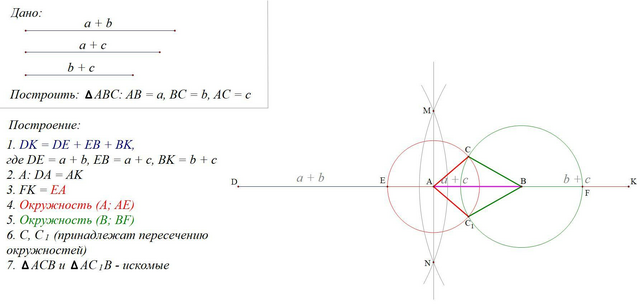
Построение во вложении.
Остановимся подробнее на построении:
1. Отрезок DK = DE + EB + BK = a + b + a + c + b + c = 2a + 2b + 2c = 2(a + b + c)
2. Точка A -- середина DK ⇒ DA = 1/2 * DK = a + b + c
Точка A строиться следующим образом:
Чертим окружности из концов отрезка (D и K) произвольного радиуса R (визуально больше половины). Эти окружности пересекутся в двух точках (M и N). Далее проводим M. Пересечение MN и DK -- искомая середина.
3. Далее смотрим на отрезки DA и DE. DA = a + b + c, DE = a + b, тогда
EA = AD - DE = a + b + c - a - b = c
То есть отрезок EA имеет длину с -- одной из сторон треугольника.
4. Затем смотрим на отрезки EB и EA. EB = a + c, EA = c, тогда
AB = EB - EA = a + c - c = a
То есть отрезок AB имеет длину a -- ещё одной из сторон треугольника.
5. Осталось найти сторону b. Для этого от точки K откладываем отрезок длиною c.
Cмотрим на отрезки BK и FK. BK = b + c, FK = c, тогда
BF = BK - FK = b + c - c = b
Получаем, что отрезок BF имеет длину b -- третья сторона треугольника.
6. Зная три стороны, можно построить искомый треугольник.
В данной задаче имеется два решения, они оба изображены на рисунке.
Для наглядности красным выделены отрезки длиною c, а также окружность радиуса c; зелёным -- длиною b. Розовым выделена сторона длиною a.