У прямокутнику ABCD AB:BC=1:3. Знайдіть площу квадрата, у якого периметр дорівнює...

Ответ:

144 $cm^{2}$

Пошаговое объяснение:

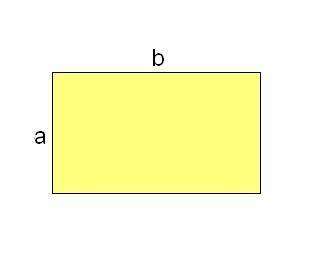
Пусть:

а = AB и a = x

b = BC

Из условия b = 3 a

Площадь прямоугольника = a * b

x * 3x = 108

Разделим обе стороны уравнения на 3.

$x^{2}$ = 36

Отсюда получаем x = 6

Периметр прямоугольника = 2a + 2b

2 * 6 + 2 * ( 6 *3 ) = 2 * 6 + 2 * 18 = 48 см

Периметр квадрата = Периметру прямоугольника

У квадрата все стороны равны, следовательно сторона квадрата равна:

48 / 4 = 12 см

Площадь квадрата = $a^{2}$ = $12^{2}$ = 144 $cm^{2}$