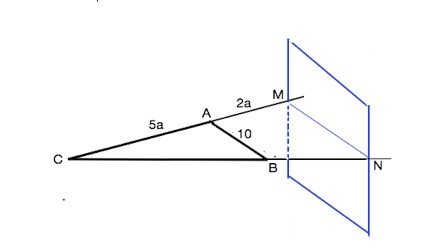
Теорема: Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
В данном случае плоскость, которой принадлежит ∆ АВС, проходит через АВ, параллельную другой плоскости и пересекает её, поэтому линия MN пересечения этих плоскостей параллельна АВ.
Плоскость, параллельная АВ, пересекает не сами стороны, а продолжения сторон АС и ВС, поэтому проходит вне треугольника, МС=АМ+АС, и МN > AB (см. рисунок)
Примем коэффициент отношения АМ:АС=а.
Тогда АС=5а, АМ=2а, а АМ=5а+2а=7а.
Плоскость параллельна АВ, следовательно, пересекает плоскость, в которой лежит треугольник, по прямой, параллельной АВ.
Соответственные углы при пересечении параллельных прямых АВ и MN секущими АМ и СN равны. ⇒ ∆ АВС~∆ AMN ( их углы равны).
Из подобия следует отношение:
АМ:АС=MN:AB
7a:5a=MN:10⇒
MN=70:5=14 (ед. длины)