Ответ:
1)Площадь боковой поверхности конуса равна 48π, а площадь основания равна 36π. Найдите длину образующей конуса.
-8
2)Площадь боковой поверхности конуса равна 48π, а площадь боковой поверхности усеченного конуса с такими же основанием и углом наклона образующей к плоскости основания равна 36π. Найдите высоту усеченного конуса, если высота исходного конуса равна 10.
Объяснение:
1)Если радиус окружности, лежащей в основании конуса обозначить за r, а длину образующей за l, то площадь основания и площадь боковой поверхности конуса выразятся по формулам: Sосн.=πr2, Sбок.пов.=πrl. Из первой формулы следует: πr2=36π ⇒ r2=36 ⇒ r=6 ⇒ 6πl=48π ⇒ 6l=48 ⇒ l=8.
2)Площадь боковой поверхности меньшего конуса, который дополняет усеченный конус до полного, равна разности их площадей поверхностей: Sмал=48π−36π=12π. Отношение площадей боковых поверхностей большого и малого конусов равно квадрату коэффициента подобия между ними: б о л м а л SболSмал=k2=48π12π=4⇒k=2 Тогда высоты конусов относятся друг к другу: hбол/hмал=10/hмал=k=2. Тогда hмал=5 ⇒hусеч=hбол-hмал=10-5=5
мал-малого,
бол-большого,усеч-усечённого
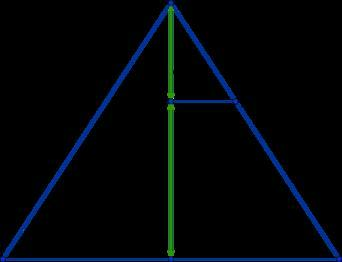
Рисунок для задачи 2)
СЛева от середины-hбольшее
Справа снизу-hусечённое
Справа вверху-hмалое