Ответ: 20 учёных не знают ни одного языка.
Пошаговое объяснение:
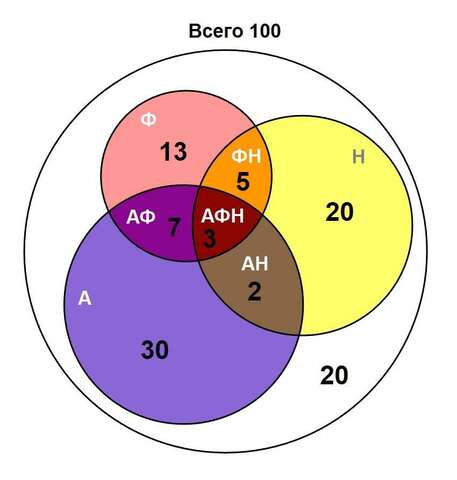
Круги Эйлера во вложении.
Пусть А, Ф, Н -- это английский, французский и немецкий языки соответсвенно.
1 способ
1. На диаграмме Эйлера изображается 4 окружности. Первая самая большая, она обозначает всех участников, всего их 100.
Затем изображается три окружности, которые попарно пересекаются. В результате образуется 8 областей, они окрашены в разные цвета:
1) Белая -- учёные, которые не знают А, Ф, Н;
2) Розовая Ф -- учёные, которые знают только Ф;
3) Жёлтая Н -- только Н;
4) Сиреневая А -- только А;
5) Фиолетовая АФ -- учёные, которые знают только А и Ф;
6) Коричневая АН -- только А и Н;
7) Оранжевая ФН -- только Ф и Н;
8) Красная АФН -- учёные, которые знают все три языка: А, Ф, Н.
2. Из них по условию дана только одна, АФН (остальные числа из условия представляют сразу несколько областей). Значит в АФН вписываем число 3.
3. Заполняем области АФ, ФН, АН
По условию Ф и Н знают 8 человек, под эту характеристику подходят две области: ФН и АФН. Значит оранжевая и красная области вместе дадут 8, тогда ФН + АФН = 8 ⇒ ФН = 8 - АФН = 8 - 3 = 5.
Аналогично находим АФ и АН:
АФ = 10 - АФН = 10 - 3 = 7
АН = 5 - АФН = 5 - 3 = 2
4. Заполняем области Ф, Н, А.
По условию Ф знают 28 человек, под эту характеристику подходят четыре области: Ф, АФ, ФН и АФН. Значит вместе они дадут 28, то есть Ф + АФ + ФН + АФН = 28 ⇒ Ф = 28 - АФ - ФН - АФН = 28 - 7 - 5 - 3 = 13.
Аналогично находим А и Н:
А = 42 - АФ - АН - АФН = 42 - 7 - 2 - 3 = 30
Н = 30 - ФН - АН - АФН = 30 - 5 - 2 - 3 = 20
5. Находим белую область. Для этого нужно вычесть из общего числа все "цветные" области, получим:
100 - Ф - А - Н - АФ - ФН - АН - АФН = 100 - 13 - 30 - 20 - 7 - 5 - 2 - 3 = 100 - 20 - 50 - 10 = 20 учёных не знают ни одного языка из предложенных.
2 способ:
Также можно привести другое решение, оно быстрее, но требует больше устных размышлений. Введён новые обозначения прямо по условию:
Х -- искомое число учёных, не знающих А, Ф, или Н;
А = 42 -- учёные знают английский, Н = 30 -- знают немецкий, Ф = 28 -- знают французский;
АН = 5 -- учёные знают А и Н, АФ = 10 -- знают А и Ф, ФН = 8 -- знают Ф и Н;
АФН -- учёные знают три языка: А, Ф, и Н.
Размышления следующие:
1) Сложим Ф и А, тогда мы дважды учтём АФ, следовательно их количество нужно вычесть один раз: (Ф + А - АФ) -- число учёных, знающих только А, только Ф и эти языки вместе.
2) Прибавим к ним Н, тогда мы снова дважды учли ФН (уже включена в Ф) и АН (уже включена в А), поэтому нужно вычесть их по одному разу, однако, при вычитании ФН и АН мы дважды вычли АФН, то есть исключили людей, знающих 3 языка. Чтобы воостановить ситуацию, прибавляем один раз АФН: (А + Ф - АФ + Н - АН - ФН + АНФ) -- число учёных, знающих какой-либо язык из А, Ф и Н.
3) Далее для поиска Х, найденную сумму во втором пункте мы вычитаем из 100. В общем виде получится такое выражение:
Х = 100 - (А + Ф - АФ + Н - АН - ФН + АНФ) = 100 - (42 + 28 - 10 + 30 - 5 - 8 + 3) = 100 - 80 = 20 учёных не знают ни одного языка из предложенных.